题目内容
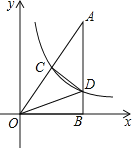
【题目】如图,已知平行四边形AOBC的顶点O(0,0),A(-3,4),点B在x轴正半轴上,按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于![]() DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G.则点G的坐标为( )
DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G.则点G的坐标为( )
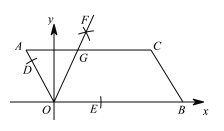
A.(2,4)B.(5,4)C.(-2,4)D.(3,4)
【答案】A
【解析】
先利用勾股定理计算出OA=5,再利用基本作图和平行线的性质得到∠AOG=∠AGO,则AG=AO=5,从而得到G点坐标.
设AC与y轴交于M点,如图:
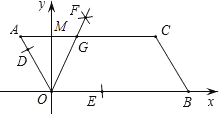
∵AOBC的顶点A的坐标为(-3,4),
∴AC∥OB, AM=3,OM=4,OA=![]() =5,
=5,
由作法得OG平分∠AOB,
∴∠AOG=∠BOG,
而AC∥OB,
∴∠AGO=∠BOG,
∴∠AOG=∠AGO,
∴AG=AO=5,
∴MG=5-3=2,
∴G点坐标为(2,4).
故选:A.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
【题目】某公司共有![]() 三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求这个公司平均每人所创年利润.