题目内容
【题目】如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AEBC=BDAC;
(2)如果![]() =3,
=3,![]() =2,DE=6,求BC的长.
=2,DE=6,求BC的长.
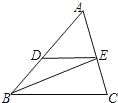
【答案】(1)证明详见解析;(2)10.
【解析】
试题分析:(1)由BE平分∠ABC交AC于点E,ED∥BC,可证得BD=DE,△ADE∽△ABC,然后由相似三角形的对应边成比例,证得AEBC=BDAC;
(2)根据三角形面积公式与![]() =3,
=3,![]() =2,可得AD:BD=3:2,然后由平行线分线段成比例定理,求得BC的长.
=2,可得AD:BD=3:2,然后由平行线分线段成比例定理,求得BC的长.
试题解析:(1)∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵DE∥BC,
∴∠DEB=∠CBE,
∴∠ABE=∠DEB,
∴BD=DE,
∵DE∥BC,
∴△ADE∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴AEBC=BDAC;
(2)解:设△ABE中边AB上的高为h,
∴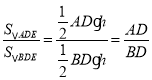 =
=![]() ,
,
∵DE∥BC,
∴![]() ,
,
∴![]() ,
,
∴BC=10.

练习册系列答案
相关题目