题目内容
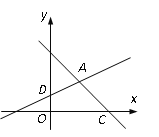
【题目】如图，在平面直角坐标系xOy中，直线y＝－x＋3与x轴交于点C，与直线AD交于点A(
， 
)，点D的坐标为（0，1）．
（1）求直线AD的解析式；
（2）直线AD与x 轴交于点B，若点E是直线AD上一动点（不与点B重合），当△BOD与△BCE相似时，求点E的坐标．
【答案】（1）求直线AD的解析式y=
x+1；（2）点E的坐标(2，2)或(3， 
)．
【解析】试题分析：
(1) 利用点A和点D的坐标，结合一次函数的一般形式，通过待定系数法获得关于待定系数的方程，求解这些方程进而可以写出直线AD的解析式.
(2) 根据题意和相似三角形的相关知识可知，本小题应按∠BOD=∠BEC=90°和∠BOD=∠BCE=90°分为两种情况进行讨论. 在第一种情况下，可以过点E作x轴的垂线EF，利用相似三角形的关系，求得线段EC的长，进而在Rt△EFC中利用勾股定理和点E的坐标特征获得相关的方程，求解这一方程即可获得点E的坐标. 在第二种情况下，可以利用EC垂直于x轴的关系直接得到点E的横坐标值，将点E的横坐标代入直线AD的解析式即可得到点E的纵坐标值，进而写出点E的坐标.
试题解析：
(1) 设直线AD的解析式为y=kx+b (k≠0).
将点A和点D的坐标分别代入直线AD的解析式，得
，
解之，得
，
∴直线AD的解析式为
.
(2) 根据题意，分别对下面两种情况进行讨论.
①∠BOD=∠BEC=90°，即△BOD∽△BEC.
如图①，过点E作EF⊥BC，垂足为F.
设点E的坐标为(m, n).
∵点E在直线AD上，
∴
.
∴点E的坐标为(m, 
).
∴OF=m，EF=
.
∵直线y=-x+3与x轴交于点C，
又∵当y=0时，-x+3=0，即x=3，
∴点C的坐标为(3, 0)，
∴OC=3.
同理，点B的坐标为(-2, 0).
∴OB=2.
∴BC=OB+OC=2+3=5.
∵点D的坐标为(0, 1)，
∴OD=1.
∴在Rt△BOD中， 
.
∵△BOD∽△BEC，
∴
.
∴
.
∵OF=m，EF=
.
∴FC=OC-OF=3-m.
∵在Rt△EFC中，EC2=EF2+FC2，
∴
，
∴m=2.
∴
.
∴点E的坐标为(2, 2).
②∠BOD=∠BCE=90°，即△BOD∽△BCE.
设点E的坐标为(m, n).
∵∠BCE=90°，OC=3，
∴m=3.
∵点E在直线AD上，
∴当m=3时， 
.
∴点E的坐标为(3, 
).
综上所述，点E的坐标为(2, 2)或(3, 
).
