题目内容
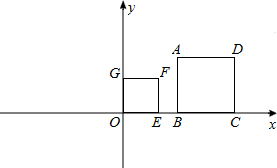（2010•安庆二模）如图，正方形OEFG和正方形ABCD的是位似图形，若点A的坐标为（2，2），位似中心的坐标是（-4，0），则点F的坐标为（
，
）
| 4 |
| 3 |
| 4 |
| 3 |
（
，
）
．| 4 |
| 3 |
| 4 |
| 3 |
分析：利用两个位似图形的主要特征是：每对位似对应点与位似中心共线；不经过位似中心的对应线段平行．则位似中心就是两对对应点的延长线的交点，得出△PFE∽△PDC，
即可求出．
即可求出．
解答：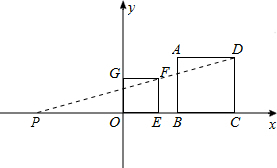
解：连接DF并延长到x轴一点P，即为位似中心，
∵正方形ABCD，点A的坐标为（2，2），
∴AB=BC=CD=AD=2，
∴OC=4，
∵EF∥DC，
∴△PFE∽△PDC，
∴
=
，
∴
=
，
又∵EO=EF，
解得：EF=
，
∴F点的坐标是（
，
）．
故答案为：（
，
）．
解：连接DF并延长到x轴一点P，即为位似中心，∵正方形ABCD，点A的坐标为（2，2），
∴AB=BC=CD=AD=2，
∴OC=4，
∵EF∥DC，
∴△PFE∽△PDC，
∴
| PE |
| PC |
| EF |
| DC |
∴
| 4+EO |
| 4+4 |
| EF |
| 2 |
又∵EO=EF，
解得：EF=
| 4 |
| 3 |
∴F点的坐标是（
| 4 |
| 3 |
| 4 |
| 3 |
故答案为：（
| 4 |
| 3 |
| 4 |
| 3 |
点评：本题主要考查了位似图形的性质以及正方形的性质和相似三角形的判定与性质等知识，利用已知得出△PFE∽△PDC是解题关键．
练习册系列答案
相关题目