Question

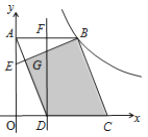
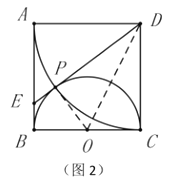
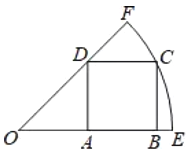
【题目】如图，正方形ABCD的四个顶点分别在扇形OEF的半径OE、OF和弧EF上，且点A是线段OB的中点，若弧EF的长为π，则OD长为______________

Answer 1

【答案】

【解析】

根据正方形的性质且点A是线段OB的中点得到OA=AD，得到∠AOD=45°，根据弧EF的长为π，求出半径OE，连接OC，利用勾股定理求出OA，再利用勾股定理即可得到OD.

在正方形ABCD中，AB=AD，∠DAB=∠ABC=90°，

∴∠OAD=90°，

∵点A是线段OB的中点，

∴OA=AB=AD，

∴∠AOD=45°，

∵弧EF的长为π，

∴,

∴OE=，

连接OC，则OC= OE=，

设OA=x，则OB=2x，BC=x，

∴，

解得x=4，

∴OD==,

故答案为：.