题目内容
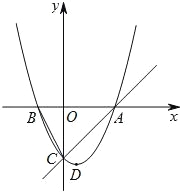
【题目】如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,﹣![]() ),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
(1)求抛物线所对应的二次函数的表达式.
(2)若动点P满足∠PAO不大于45°,求P点的横坐标m的取值范围.
(3)是否存在P点,使∠PAC=∠BCO?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)抛物线为y=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() ;
;
(2)﹣4≤m≤0;
(3)存在,当点P坐标(﹣1,﹣![]() )或(﹣3,
)或(﹣3,![]() )时,∠PAC=∠BCO.
)时,∠PAC=∠BCO.
【解析】
试题分析:(1)设抛物线为y=a(x﹣1)2﹣![]() ,把点(4,0)代入即可解决问题.
,把点(4,0)代入即可解决问题.
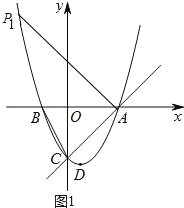
(2)如图1中,求出∠PAO=45°时点P的坐标,由此即可解决问题.
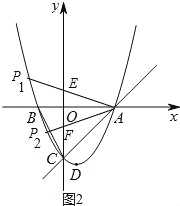
(3)存在.如图2中,∠P1AO=∠BCO,设AP1交y轴于E,理由相似三角形求出OE的长,再求出直线CE与抛物线的交点即可解决问题,根据对称性再求出P2坐标即可.
试题解析:(1)设抛物线为y=a(x﹣1)2﹣![]() ,
,
∵抛物线经过点(4,0),
∴0=9a﹣![]() ,
,
∴a=![]() ,
,
∴抛物线为y=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() .
.
(2)∵y=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() .
.
令x=0,则y=﹣4,∴点C坐标(0,﹣4),
令y=0,(x﹣1)2=9,解得x=﹣2或4,
∴点B坐标(﹣2,0),点A坐标(4,0).
∴OA=OC,
∴∠OAC=∠OCA=45°,
如图1中,过点A作直线AP1⊥AC,交抛物线于P1,
∵直线AC为y=x﹣4,
∴直线AP1为y=﹣x+4,
由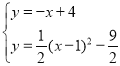 ,解得
,解得![]() 或
或![]() ,
,
∴点P1坐标(﹣4,8),
∴当点P在P1与C之间时,∠PAO不大于45°,
∴﹣4≤m≤0.
(3)存在.
理由:如图2中,∠P1AO=∠BCO,设AP1交y轴于E,
∵△BCO∽△EAO,
∴![]() ,
,
∴![]() ,
,
∴EO=2,
∴点E坐标(0,2),
∴直线AE为y=﹣![]() x+2,
x+2,
由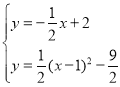 解得
解得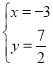 或
或![]() ,
,
∴p1(﹣3,![]() ).
).
根据对称性∠P2AO=∠BCO时,设AP2交y轴于F,则点F坐标(0,﹣2),
∴直线AF为y=![]() x﹣2,
x﹣2,
由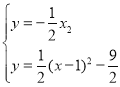 解得
解得![]() 或
或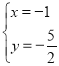 ,
,
∴点P2(﹣1,﹣![]() ).
).
∴当点P坐标(﹣1,﹣![]() )或(﹣3,
)或(﹣3,![]() )时,∠PAC=∠BCO.
)时,∠PAC=∠BCO.