题目内容
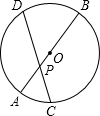如图：已知P为⊙O直径AB上任意一点，弦CD过P且与AB交成45°角．求证：PC2+PD2为定值．
证明：当点p与O点重合时，PC2+PD2=2圆O的半径的平方
当点P为一般情况时，
作CM⊥AB于M，DN⊥AB于N，连接OC和OD，
可知∠NDP=∠MCP=45°
又OC=OD，则∠ODP=∠OCP
∴∠NDO=∠COM
∴Rt△ODN≌Rt△COM
∴ON=CM=PM，OM=ND=PN
又∵OC2=CM2+OM2，OD2=DN2+ON2
∴OC2=CM2+PN2，OD2=DN2+PM2
∴OC2+OD2=CM2+PN2+DN2+PM2=PC2+PD2，
因此PC2+PD2=2圆O的半径的平方（为定值）．
分析：分类讨论（1）P点与O点重合，（2）P为一般情况，求证Rt△ODN≌Rt△COM，得ON=CM=PM，OM=ND=PN，从而求证OC2+OD2=PC2+PD2为定值．
点评：本题考查了在圆中构建三角形运用勾股定理解直角三角形，本题中求证PC2+PD2=2OC2是解题的关键．
练习册系列答案
相关题目
如图，已知抛物线C1与坐标轴的交点依次是A（-4，0），B（-2，0），E（0，8）．
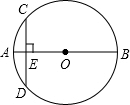如图，已知⊙O的直AB=20cm，CD垂AB于E，CD=12cm，AE的长为（ ）| A、1cm | B、2cm | C、3cm | D、4cm |
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=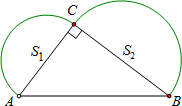
（2012•咸丰县二模）如图，已知在Rt△ABC中，∠ACB=90°，AB=10，分别以AC、BC为直经作半圆，面积分别记为S1、S2，则S1+S2的值等于（ ）
如图，已知直l1∥l2∥l3∥l4，相邻两条平行直线间的距离都是2，如果正方形ABCD的四个顶点分别在四条直线上，则正方形边长的值为