题目内容
 想一想,将下列解题过程补充完整.
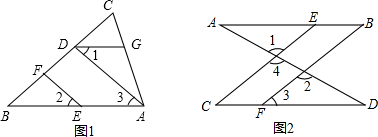
想一想,将下列解题过程补充完整.如图1,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,所以∠2=
∠3
∠3
.(两直线平行,同位角相等)
(两直线平行,同位角相等)
又因为∠1=∠2,所以∠1=∠3.
所以AB∥
DG
DG
.(内错角相等,两直线平行)
(内错角相等,两直线平行)
所以∠BAC+
∠DGA
∠DGA
=180°.又因为∠BAC=70°,
所以∠AGD=
110°
110°
.如图2,已知∠1=∠2,∠B=∠C,试说明AB∥CD.
解:∵∠1=∠2(已知),
又∵∠1=∠4
(对顶角相等)
(对顶角相等)
∴∠2=∠
4
4
(等量代换)∴
CE
CE
∥BF(同位角相等,两直线平行)
(同位角相等,两直线平行)
∴∠
C
C
=∠3(两直线平行,同位角相等)
(两直线平行,同位角相等)
又∵∠B=∠C(已知)
∴∠
3
3
=∠B(等量代换)∴AB∥CD
内错角相等,两直线平行)
内错角相等,两直线平行)
.分析:(1)根据平行线的性质可得∠2=∠3,再根据∠1=∠2可得∠1=∠3,进而证出AB∥DG,再根据两直线平行,同旁内角互补可得∠AGD的度数;
(2)首先证明CE∥BF,可得∠C=∠3,再根据∠B=∠C可得∠3=∠B,再证明AB∥CD即可,
(2)首先证明CE∥BF,可得∠C=∠3,再根据∠B=∠C可得∠3=∠B,再证明AB∥CD即可,
解答:解:(1)因为EF∥AD,所以∠2=∠3. (两直线平行,同位角相等)
又因为∠1=∠2,所以∠1=∠3.
所以AB∥DG. (内错角相等,两直线平行)
所以∠BAC+∠DGA=180°.
又因为∠BAC=70°,
所以∠AGD=110°.
(2)∵∠1=∠2(已知),
又∵∠1=∠4 (对顶角相等)
∴∠2=∠4(等量代换)
∴CE∥BF (同位角相等,两直线平行)
∴∠C=∠3 (两直线平行,同位角相等)
又∵∠B=∠C(已知)
∴∠3=∠B(等量代换)
∴AB∥CD 内错角相等,两直线平行).
又因为∠1=∠2,所以∠1=∠3.
所以AB∥DG. (内错角相等,两直线平行)
所以∠BAC+∠DGA=180°.

又因为∠BAC=70°,
所以∠AGD=110°.
(2)∵∠1=∠2(已知),
又∵∠1=∠4 (对顶角相等)
∴∠2=∠4(等量代换)
∴CE∥BF (同位角相等,两直线平行)
∴∠C=∠3 (两直线平行,同位角相等)
又∵∠B=∠C(已知)
∴∠3=∠B(等量代换)
∴AB∥CD 内错角相等,两直线平行).
点评:此题主要考查了平行线的判定与性质,关键是熟练掌握判定定理与性质定理.

练习册系列答案
相关题目

 •
• •
• •
•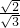 =
=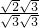 =
= .
.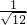 =______=______;②
=______=______;②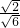 =______=______;
=______=______; ﹢
﹢ -3)(______)使其结果不再含有根号;同样请你仿照(1)的方法将下列二次根式化简:
-3)(______)使其结果不再含有根号;同样请你仿照(1)的方法将下列二次根式化简: .
.