Question

已知：如图AB∥CD，AD∥CE，且∠ACB=90º，E是AB的中点． 

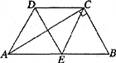
(1)试说明DE与AC互相垂直平分；

(2)探究l，当四边形AECD是正方形时，∠B的度数是多少?

(3)探究2，当四边形ABCD是等腰梯形时，∠B的度数是多少?

Answer 1

解：(1)因为AB∥CD，AD∥CE，所以四边形AECD是平行四边形．

  在△ABC中，E是AB的中点，

  所以CE=EA=EB，

  所以平行四边形AECD是菱形，所以DE与AC互相垂直平分．

(2)当四边形AECD是正方形时，CE⊥AB．

  因为EA=EB，所以CA=CB

  因为∠ACB=90°，

  所以△ACB是等腰直角三角形，所以∠B=45°

(3)当四边形ABCD是等腰梯形时，AD=BC．

  因为AD=CE=EB，所以CE=EB=BC，

  所以△EBC是等边三角形，所以∠B=60°