��Ŀ����
����Ŀ�����ⱳ�����ڡ�ABC�У���B=2��C����DΪ�߶�BC��һ���㣬��AD����ij������ʱ��̽�����߶�AB��BD��CD��AC�����߶��У�ij������ij�����߶�֮����ڵ�������ϵ��
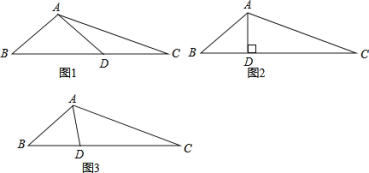
���磺��ͼ1�У���AB=ADʱ����֤��AB=DC�����ڼ���̽����
����Ҫ��
��1����AD��BCʱ����ͼ2����֤��AB+BD=DC��
��2����AD�ǡ�BAC�Ľ�ƽ����ʱ���ж�AB��BD��AC��������ϵ����֤����Ľ��ۡ�
���𰸡���1��֤������⣻
��2��AB+BD=AC��
��������
��1��������������DC�Ͻ�ȡDM=BD������AM������ȫ�������Ρ�ABD�ա�AMD��Ȼ����ȫ�������εĶ�Ӧ������Լ����������ε�����֤�á�B=��AMB��������֪��������������Ƕ�����á�C=��MAC������AM=MC�������ݵ����������MC=AB����AB+BD=DC��
��2���ӳ�AB��M��ʹBM=BD������MD����ABD=��M+��BDM=2��M���ɡ�ABD=2��C���á�M=��C����֤��AMD�ա�ACD���ɵý���AB+BD=AC��
�⣺
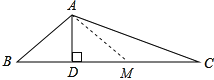
��1����DC�Ͻ�ȡDM=BD������AM��
����ABD����AMD��
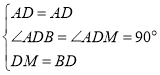 ��
��
���ABD�ա�AMD��SAS����
��AB=AM��
���B=��AMB��
�ߡ�AMD=��MAC+��C����B=2��C��
���C=��MAC��
��AM=MC��
��MC=AB��
��AB+BD=DC��
��2��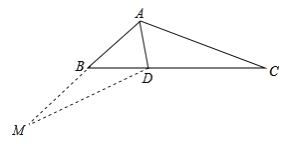
��ͼʾ���ӳ�AB��M��ʹBM=BD������MD��
���ABD=��M+��BDM=2��M��
�ߡ�ABD=2��C��
���M=��C��
�֡�AD�ǡ�BAC�Ľ�ƽ���ߣ�
���BAD=��CAD��
AD=AD�������ߣ�
���AMD�ա�ACD��AAS����
��AM=AC��
��AB+BD=AC��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�