题目内容
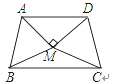
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.

【答案】DE=BF,DE⊥BF.理由见解析.
【解析】试题分析:本题首先要给出答案,在说明理由. 连接DB,根据DH是AB的垂直平分线得出∠A=∠DBH,再根据三角形外角的性质得出∠CDB=∠A+∠DBH,故可得出CD=CB.由SAS定理得出△ECD≌△FCB,所以ED=FB,∠DEC=∠BFC,∠DEC+∠FBC=90°,进而可得出结论.
试题解析:
DE=BF,DE⊥BF.
理由如下:
连接BD,延长BF交DE于点G.
∵点D在线段AB的垂直平分线上,∴AD=BD,
∴∠ABD=∠A=22.5°.
在Rt△ABC中,∵∠ACB=90°,∠A=22.5°,
∴∠ABC=67.5°,
∴∠CBD=∠ABC-∠ABD=45°,
∴△BCD为等腰直角三角形,
∴BC=DC.
又∵CE=CF,∴Rt△ECD≌Rt△FCB(SAS),
∴DE=BF,∠CED=∠CFB.
∵∠CFB+∠CBF=90°,∴∠CED+∠CBF=90°,
∴∠EGB=90°,即DE⊥BF.


练习册系列答案
相关题目