Question

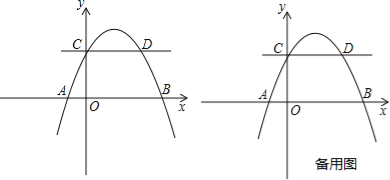
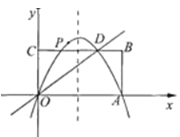
【题目】矩形OABC在直角坐标系中的位置如图所示，A、C两点的坐标分别为A(6，0)、C(0，3)，直线y=x与BC边相交于D．

（1）求点D的坐标：

（2）若抛物线y=ax＋bx经过D、A两点，试确定此抛物线的表达式：

（3）P为x轴上方（2）题中的抛物线上一点，求△POA面积的最大值．

Answer 1

【答案】（1）(4，3)；（2）y=x+x；（3）

【解析】

（1）根据矩形的性质可知点D的纵坐标为3，代入直线解析式即可求出点D的横坐标，从而可确定点D的坐标；

（2）直接将点A、D的坐标代入抛物线解析式即可；

（3）当P为抛物线顶点时，△POA面积最大，将抛物线解析式化为顶点式，求出点P的坐标，再计算面积即可．

解：（1）设D的横坐标为x,则根据题意有3=x，则x=4

∴D点坐标为（4，3）

（2）将A（6，0），D(4,3)代入y=ax＋bx中，得

解得：

∴此抛物线的表达式为：y=x+x；

（3）由于△POA底边为OA=6，

∴当P为抛物线顶点时，△POA面积最大

∴

∴

∴的最大值为