题目内容
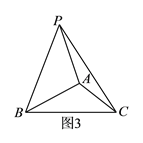
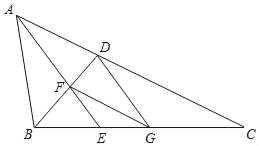
【题目】如图,已知在△ABC中,∠BAC=2∠C,∠BAC的平分线AE与∠ABC的平分线BD相交于点F,FG∥AC,联结DG.
(1)求证:BFBC=ABBD;
(2)求证:四边形ADGF是菱形.
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)通过证明△ABF∽△CBD,由相似三角形对应边成比例即可得出结论;
(2)先证明△ABF≌△GBF,得到AF=FG,BA=BG,再证明△ABD≌△GBD,得到∠BAD=∠BGD,进而得到AF∥DG,从而有四边形ADGF是平行四边形,根据邻边相等的平行四边形是菱形即可得到结论.
试题解析:证明:(1)∵AE平分∠BAC,∴∠BAC=2∠BAF=2∠EAC.
∵∠BAC=2∠C,∴∠BAF=∠C=∠EAC.又∵BD平分∠ABC,∴∠ABD=∠DBC.
∵∠ABF=∠C,∠ABD=∠DBC,∴△ABF∽△CBD,∴![]() ,∴BFBC=ABBD.
,∴BFBC=ABBD.
(2)∵FG∥AC,∴∠C=∠FGB,∴∠FGB=∠FAB.
∵∠BAF=∠BGF,∠ABD=∠GBD,BF=BF,∴△ABF≌△GBF,∴AF=FG,BA=BG.
∵BA=BG,∠ABD=∠GBD,BD=BD,∴△ABD≌△GBD,∴∠BAD=∠BGD.
∵∠BAD=2∠C,∴∠BGD=2∠C,∴∠GDC=∠C,∴∠GDC=∠EAC,∴AF∥DG.
又∵FG∥AC,∴四边形ADGF是平行四边形,∴AF=FG,∴四边形ADGF是菱形.

练习册系列答案
相关题目