题目内容
【题目】(![]() )探究发现
)探究发现
下面是一道例题及其解答过程,请补充完整:
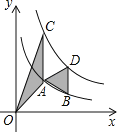
如图①在等边![]() 内部,有一点
内部,有一点![]() ,若
,若![]() ,求证:
,求证: ![]() ,
,
证明:将![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,则
,则![]() 为等边三角形.
为等边三角形.
∴![]() ,
, ![]() ,
, ![]() __________.
__________.
∵![]() ,∴
,∴![]() ,
,
∴![]() __________,
__________,
即![]() ,
,
(![]() )类比延伸:
)类比延伸:
如图②在等腰三角形![]() 中,
中, ![]() ,内部有一点
,内部有一点![]() ,若
,若![]() ,试判断线段
,试判断线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
(![]() )联想拓展:
)联想拓展:
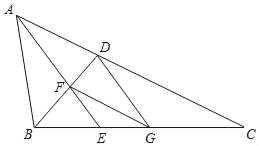
如图③在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 在直线
在直线![]() 上方,且
上方,且![]() ,满足
,满足![]() ,请直接写出
,请直接写出![]() 的值.
的值.

【答案】 ![]()
![]()
【解析】试题分析:(1)根据旋转的性质和勾股定理直接写出即可;
(2)将![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,论证
,论证![]()
再根据勾股定理代换即可;
(3)将![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,
,
论证![]() 再根据勾股定理代换即可.
再根据勾股定理代换即可.
试题解析:(![]() )探究发现:
)探究发现:
![]() ,
, ![]() .
.
(![]() )关系式为:
)关系式为: ![]() .
.
将![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,
,
则![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
, ![]() ,
, ![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
(![]() )将
)将![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到
得到![]() ,
,
连接![]() ,过点
,过点![]() 作
作![]() ,
,

可得![]() ,
, ![]() ,
, ![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司一共62辆![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人/辆 | 380元/辆 |
| 20人/辆 | 280元/辆 |
注:载客量指的是每辆客车最多可载该校师生的人数.设学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案总费用最省?最省的总费用是多少?