Question

【题目】问题情景：如图1，中，有一块直角三角板放置在上（点在内），使三角板的两条直角边、恰好分别经过点和点.

试问与是否存在某种确定的数量关系？

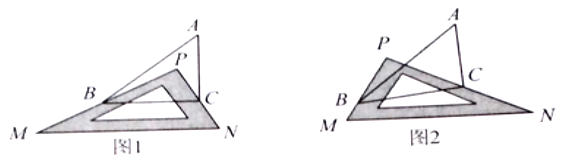
（1）特殊研究：若，则 度， 度， 度；

（2）类比探索：请探究与的关系.

（3）类比延伸：如图2，改变直角三角包的位置；使点在外，三角板的两条直角边、仍然分别经过点和点，（2）中的结论是否仍然成立？若不成立请直接写出你的结论.

Answer 1

【答案】（1）140，90，50；（2）结论：∠ABP+∠ACP＝90°﹣∠A，理由详见解析；（3）不成立，存在结论：∠ACP﹣∠ABP＝90°﹣∠A．

【解析】

（1）已知，根据三角形的内角和定理求出的度数，已知∠P=90°，根据三角形的内角和定理求出的度数，进而得到的度数；

（2）由（1）中的度数，的度数，相减即可得到与∠A的关系；

（3）在△ABC中，=180°-∠A，同理在△PBC中，=90°，相减可得到∠ACP﹣∠ABP＝90°﹣∠A．

解：（1）∵

∴=180°-∠A=140°，

∵∠P=90°，

∴=90°，

∴=140°-90°=50°，

（2）结论：∠ABP+∠ACP＝90°﹣∠A．

证明：∵90°+（∠ABP+∠ACP）+∠A＝180°，

∴∠ABP+∠ACP+∠A＝90°，

∴∠ABP+∠ACP＝90°﹣∠A．

（3）不成立；存在结论：∠ACP﹣∠ABP＝90°﹣∠A．

理由：在△ABC中，=180°-∠A，

在△PBC中，∠P=90°，∴=90°，

∴（）-（）=180°-∠A-90°，

即=90°﹣∠A．

∴∠ACP﹣∠ABP＝90°﹣∠A．