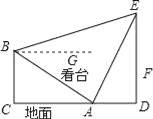
ЬтФПФкШн
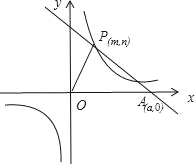
ЁОЬтФПЁПШчЭМЃЌдкГЄЗНаЮOABCжаЃЌOЮЊЦНУцжБНЧзјБъЯЕЕФдЕуЃЌЕуAЕФзјБъЮЊЃЈaЃЌ0ЃЉЃЌЕуCЕФзјБъЮЊЃЈ0ЃЌbЃЉЧвaЁЂbТњзу![]() +|bЉ6|ЃН0ЃЌЕуBдкЕквЛЯѓЯоФкЃЌЕуPДгдЕуГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбизХOЉCЉBЉAЉOЕФЯпТЗвЦЖЏЃЎ
+|bЉ6|ЃН0ЃЌЕуBдкЕквЛЯѓЯоФкЃЌЕуPДгдЕуГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбизХOЉCЉBЉAЉOЕФЯпТЗвЦЖЏЃЎ
ЃЈ1ЃЉЕуBЕФзјБъЮЊЁЁ ЁЁЃЛЕБЕуPвЦЖЏ3.5УыЪБЃЌЕуPЕФзјБъЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉдквЦЖЏЙ§ГЬжаЃЌЕБЕуPЕНxжсЕФОрРыЮЊ4ИіЕЅЮЛГЄЖШЪБЃЌЧѓЕуPвЦЖЏЕФЪБМфЃЛ
ЃЈ3ЃЉдкOЉCЉBЕФЯпТЗвЦЖЏЙ§ГЬжаЃЌЪЧЗёДцдкЕуPЪЙЁїOBPЕФУцЛ§ЪЧ10ЃЌШєДцдкЧѓГіЕуPвЦЖЏЕФЪБМфЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
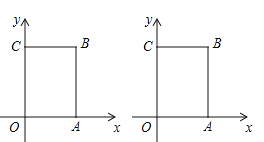
ЁОД№АИЁПЃЈ1ЃЉЃЈ4,6ЃЉЃЌЃЈ1,6ЃЉЃЛЃЈ2ЃЉ2УыЛђ6УыЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЗЧИКЪ§ЕФаджЪПЩвдЧѓЕУaЁЂbЕФжЕЃЌИљОнГЄЗНаЮЕФаджЪЃЌПЩвдЧѓЕУЕуBЕФзјБъЃЛИљОнЬтвтЕуPДгдЕуГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбизХO-C-B-A-OЕФЯпТЗвЦЖЏЃЌПЩвдЕУЕНЕБЕуPвЦЖЏ4УыЪБЃЌЕуPЕФЮЛжУКЭЕуPЕФзјБъЃЛ
ЃЈ2ЃЉгЩЬтвтПЩвдЕУЕНЗћКЯвЊЧѓЕФгаСНжжЧщПіЃЌЗжБ№ЧѓГіСНжжЧщПіЯТЕуPвЦЖЏЕФЪБМфМДПЩЃЎ
ЃЈ3ЃЉЗжЮЊЕуPдкOCЁЂBCЩЯЗжРрМЦЫуМДПЩЃЎ
ЃЈ1ЃЉЁпaЁЂbТњзу![]() +|b-6|=0ЃЌ
+|b-6|=0ЃЌ
Ёрa-4=0ЃЌb-6=0ЃЌ
НтЕУa=4ЃЌb=6ЃЌ
ЁрЕуBЕФзјБъЪЧЃЈ4ЃЌ6ЃЉЃЌ
ЁпЕуPДгдЕуГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбизХO-C-B-A-OЕФЯпТЗвЦЖЏЃЌ
Ёр2ЁС3.5=7ЃЌ
ЁпOA=4ЃЌOC=6ЃЌ
ЁрЕБЕуPвЦЖЏ4УыЪБЃЌдкЯпЖЮCBЩЯЃЌРыЕуCЕФОрРыЪЧЃК7-6=1ЃЌ
МДЕБЕуPвЦЖЏ4УыЪБЃЌДЫЪБЕуPдкЯпЖЮCBЩЯЃЌРыЕуCЕФОрРыЪЧ2ИіЕЅЮЛГЄЖШЃЌЕуPЕФзјБъЪЧЃЈ1ЃЌ6ЃЉЃЛ
ЙЪД№АИЮЊЃЈ4ЃЌ6ЃЉЃЌЃЈ1ЃЌ6ЃЉЃЎ
ЃЈ2ЃЉгЩЬтвтПЩЕУЃЌдквЦЖЏЙ§ГЬжаЃЌЕБЕуPЕНxжсЕФОрРыЮЊ4ИіЕЅЮЛГЄЖШЪБЃЌДцдкСНжжЧщПіЃЌ
ЕквЛжжЧщПіЃЌЕБЕуPдкOCЩЯЪБЃЌ
ЕуPвЦЖЏЕФЪБМфЪЧЃК4ЁТ2=2УыЃЌ
ЕкЖўжжЧщПіЃЌЕБЕуPдкBAЩЯЪБЃЎ
ЕуPвЦЖЏЕФЪБМфЪЧЃКЃЈ6+4+2ЃЉЁТ2=6УыЃЌ
ЙЪдквЦЖЏЙ§ГЬжаЃЌЕБЕуPЕНxжсЕФОрРыЮЊ4ИіЕЅЮЛГЄЖШЪБЃЌЕуPвЦЖЏЕФЪБМфЪЧ2УыЛђ6УыЃЎ
ЃЈ3ЃЉШчЭМ1ЫљЪОЃК
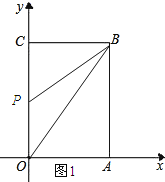
ЁпЁїOBPЕФУцЛ§=10ЃЌ
Ёр![]() OPBC=10ЃЌМД
OPBC=10ЃЌМД![]() ЁС4ЁСOP=10ЃЎ
ЁС4ЁСOP=10ЃЎ
НтЕУЃКOP=5ЃЎ
ЁрДЫЪБt=2.5s
ШчЭМ2ЫљЪОЃЛ
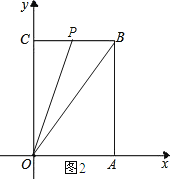
ЁпЁїOBPЕФУцЛ§=10ЃЌ
Ёр![]() PBOC=10ЃЌМД
PBOC=10ЃЌМД ![]() ЁС6ЁСPB=10ЃЎ
ЁС6ЁСPB=10ЃЎ
НтЕУЃКBP=![]() ЃЎ
ЃЎ
ЁрCP=![]() ЃЎ
ЃЎ
ЁрOC+CP=6+![]() =
=![]() ЃЌ
ЃЌ
ЁрДЫЪБt=![]() sЃЌ
sЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЪБМфtЕФжЕЮЊ2.5sЛђ![]() sЃЎ
sЃЎ

 ШЋгХПМЕфЕЅдЊМьВтОэМАЙщРрзмИДЯАЯЕСаД№АИ
ШЋгХПМЕфЕЅдЊМьВтОэМАЙщРрзмИДЯАЯЕСаД№АИ