题目内容
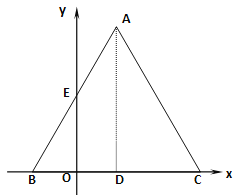
【题目】如图，矩形ABCD中，AB=6，BC=8，点E是射线CB上的一个动点，把△DCE沿DE折叠，点C的对应点为C′．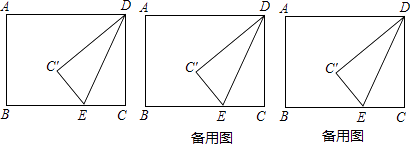
（1）若点C′刚好落在对角线BD上时，BC′=；
（2）当B C′∥DE时，求CE的长；
（3）若点C′刚好落在线段AD的垂直平分线上时，求CE的长．
【答案】
（1）4
（2）
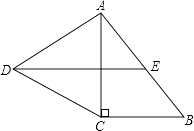
解：如图2，由折叠得，∠CED=∠C′ED，
∵BC′∥DE，
∴∠EC′B=∠C′ED，∠CED=∠C′BE，
∴∠EC′B=∠C′EB，
∴BE=C′E=EC=4；
（3）
解：作AD的垂直平分线，交AD于点M，交BC于点N，分两种情况讨论：
①当点C′在矩形内部时，如图3，
∵点C′在AD的垂直平分线上，
∴DM=4，
∵DC′=6，
∴由勾股定理得：MC′=2 
，
∴NC′=6﹣2 ，
设EC=x，则C′E=x，NE=4﹣x，
∵NC′2+NE2=C′E2，
∴（6﹣2 ）2+（4﹣x）2=x2，
解得：x=9﹣3 ，
即CE=9﹣3 ；
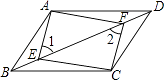
②当点C′在矩形外部时，如图4，
∵点C′在AD的垂直平分线上，
∴DM=4，
∵DC′=6，
∴由勾股定理得：MC′=2 ，
∴NC′=6+2 ，
设EC=y，则C′E=y，NE=y﹣4，
∵NC′2+NE2=C′E2，
∴（6+2 ）2+（y﹣4）2=y2，
解得：y=9+3 ，
即CE=9+3 ，
综上所述，CE的长为9±3 ．
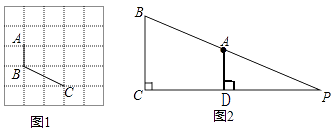
【解析】解：（1）如图1，由折叠可得DC'=DC=6，
∵∠C=90°，BC=8，
∴Rt△BCD中，BD=10，
∴BC′=10﹣6=4．
所以答案是4；
【考点精析】解答此题的关键在于理解翻折变换（折叠问题）的相关知识，掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
