题目内容
如图: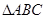 中,点
中,点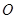 是
是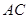 边上一动点,过点
边上一动点,过点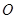 作直线
作直线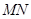 ∥
∥ ,设
,设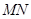 交
交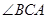 的平分线于点
的平分线于点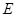 ,交
,交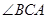 的外角平分线于点
的外角平分线于点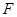 。(8分)
。(8分)
⑴求证: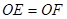 ;
;
⑵当点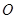 运动到
运动到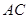 中点时,四边形
中点时,四边形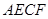 为怎样的四边形,并证明你的结论;
为怎样的四边形,并证明你的结论;
【答案】
见解析
【解析】
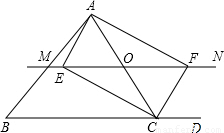
试题分析: 解:(1)证明:∵MN∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠BCE=∠ACE=∠OEC,∠OCF=∠FCD=∠OFC,
∴OE=OC,OC=OF,
∴OE=OF。
(2)当O运动到AC中点时,四边形AECF是矩形,
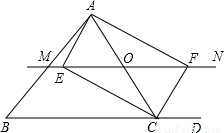
∵AO=CO,OE=OF,
∴四边形AECF是平行四边形,
∵∠ECA+∠ACF=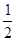 ∠BCD,
∠BCD,
∴∠ECF=90°,
∴四边形AECF是矩形。
考点:本题考查了矩形的判定定理。
点评:此类试题属于高难度试题,考生务必留意以下出题点:
(1)矩形的判定
①定义:有一个角是直角的平行四边形是矩形
②有三个角是直角的四边形是矩形
③对角线互相平分且相等的平行四边形是矩形
(2)矩形的性质定理:矩形具有平行四边形的所有性质,从而矩形的性质可归结为从三个方面来看:
①从边看,矩形对边平行且相等。
②从角看,矩形四个角都是直角。
③从对角线看,矩形对角线互相平分且相等。
④矩形具有菱形和平行四边形的一切性质
矩形是轴对称图形,它有两条对称轴,也是中心对称图形,对称中心是对角线的交点。

练习册系列答案
相关题目
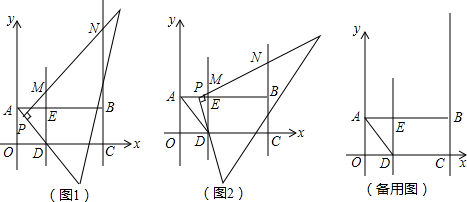



 (2014•宝山区一模)如图△ABC中,∠C=90°,∠A=30°,BC=5cm;△DEF中,∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).
(2014•宝山区一模)如图△ABC中,∠C=90°,∠A=30°,BC=5cm;△DEF中,∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).