题目内容
(2013•丰台区一模)在△ABC中,∠ACB=90°,AC>BC,D是AC边上的动点,E是BC边上的动点,AD=BC,CD=BE.

(1)如图1,若点E与点C重合,连结BD,请写出∠BDE的度数;
(2)若点E与点B、C不重合,连结AE、BD交于点F,请在图2中补全图形,并求出∠BFE的度数.

(1)如图1,若点E与点C重合,连结BD,请写出∠BDE的度数;
(2)若点E与点B、C不重合,连结AE、BD交于点F,请在图2中补全图形,并求出∠BFE的度数.
分析:(1)由CD=BE,∠ACB=90°就可以得出△BCD是等腰直角三角形,故可以得出∠BDE的度数;
(2)作AG⊥AC且AG=CD=BE,连接BG,则四边形AEBG是平行四边形.连接GD,证明Rt△BCD≌Rt△DAG,则GD=BD,△BGD是等腰直角三角形.就可以求出结论.
(2)作AG⊥AC且AG=CD=BE,连接BG,则四边形AEBG是平行四边形.连接GD,证明Rt△BCD≌Rt△DAG,则GD=BD,△BGD是等腰直角三角形.就可以求出结论.
解答:解:(1)∵点E与点C重合,
∴BE=BC.
∵CD=BE,
∴CD=BC.
∵∠ACB=90°,
∴∠BDE=45°
 (2)作AG⊥AC且AG=CD=BE,连接BG,GD,
(2)作AG⊥AC且AG=CD=BE,连接BG,GD,
∴∠GAD=90°.
∵∠ACB=90°.
∴BC⊥AC,∠GAD=∠ACB
∴AG∥BC,
∴四边形AEBG是平行四边形,
∴GB∥AE,
∴∠AFD=∠GBD.
在△GAD和△DCB中,
,
∴△GAD≌△DCB(SAS),
∴GD=BD,∠GDA=∠DBC,
∵∠DBC+∠BDC=90°,
∴∠GDA+∠BDC=90°,
∴∠GDB=90°,
∴△BGD是等腰直角三角形,
∴∠GBD=45°,
∴∠AFD=45°,
∴∠BFE=45°.
∴BE=BC.
∵CD=BE,
∴CD=BC.
∵∠ACB=90°,
∴∠BDE=45°
 (2)作AG⊥AC且AG=CD=BE,连接BG,GD,
(2)作AG⊥AC且AG=CD=BE,连接BG,GD,∴∠GAD=90°.
∵∠ACB=90°.
∴BC⊥AC,∠GAD=∠ACB
∴AG∥BC,
∴四边形AEBG是平行四边形,
∴GB∥AE,
∴∠AFD=∠GBD.
在△GAD和△DCB中,
|
∴△GAD≌△DCB(SAS),
∴GD=BD,∠GDA=∠DBC,
∵∠DBC+∠BDC=90°,
∴∠GDA+∠BDC=90°,
∴∠GDB=90°,
∴△BGD是等腰直角三角形,
∴∠GBD=45°,
∴∠AFD=45°,
∴∠BFE=45°.
点评:本题考查了等腰直角三角形的性质的运用,平行四边形的判定及性质的运用,全等三角形的判定及性质的运用,解答时添加合适的辅助线是难点,证明△BGD是等腰直角三角形是关键.

练习册系列答案
相关题目
 (2013•丰台区一模)如图,四边形ABCD中,AB=AD,∠BAD=90°,∠CBD=30°,∠BCD=45°,若AB=2
(2013•丰台区一模)如图,四边形ABCD中,AB=AD,∠BAD=90°,∠CBD=30°,∠BCD=45°,若AB=2
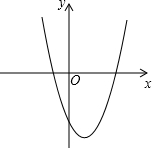 (2013•丰台区一模)二次函数y=x2+bx+c的图象如图所示,其顶点坐标为M(1,-4).
(2013•丰台区一模)二次函数y=x2+bx+c的图象如图所示,其顶点坐标为M(1,-4). (2013•丰台区一模)如图,在平面直角坐标系xOy中,⊙C的圆心坐标为(-2,-2),半径为
(2013•丰台区一模)如图,在平面直角坐标系xOy中,⊙C的圆心坐标为(-2,-2),半径为