��Ŀ����
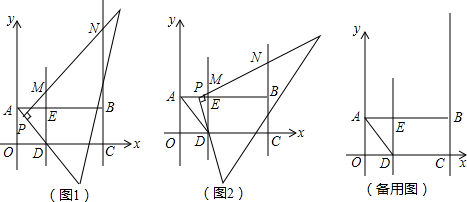
��2013•���ݣ���ͼ����ƽ��ֱ������ϵ�У�����OABC�ı�OA=2��0C=6����OC��ȡ��D����AOD��AD���ۣ�ʹO������AB���ϵ�E�㴦����һ���㹻���ֱ�����ǰ�Ķ���P��D��������߶�DA��AB�ƶ�����һֱ�DZ�ʼ�վ�����D����һֱ�DZ�����ֱ����ֱ��DE��BC�ֱ��ڵ�M��N��
��1����գ�D�������ǣ�
��2����ͼ1������P���߶�DA���ƶ�ʱ���Ƿ���������ĵ�M��ʹ��CMNΪ���������Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ2������P���߶�AB���ƶ�ʱ����P������Ϊ��x��2�����ǡ�DBN�����ΪS����ֱ��д��S��x֮��ĺ�����ϵʽ�������S��x�������Сʱ����Ӧ���Ա���x��ȡֵ��Χ��
��1����գ�D�������ǣ�
2
2
��0
0
����E�������ǣ�2
2
��2
2
������2����ͼ1������P���߶�DA���ƶ�ʱ���Ƿ���������ĵ�M��ʹ��CMNΪ���������Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ2������P���߶�AB���ƶ�ʱ����P������Ϊ��x��2�����ǡ�DBN�����ΪS����ֱ��д��S��x֮��ĺ�����ϵʽ�������S��x�������Сʱ����Ӧ���Ա���x��ȡֵ��Χ��

��������1�����ݡ�AOD��AD���ۣ�ʹO������AB���ϵ�E�㴦���õ���OAD=��EAD=45�㣬DE=OD�����OD=2���ó�D������꣬�ٸ���DE=OD=2�����E������ꣻ
��2���ɷ��ۿ�֪�ı���AODEΪ�����Σ���M��MH��BC��H���������NMH=��MNH=45�㣬�ó�NH=MH=4��MN=4
���ٸ���ֱ��OE�Ľ���ʽΪ��y=x���������MN��OE����MN�Ľ���ʽΪy=x+b������DE�Ľ���ʽΪx=2��BC�Ľ���ʽΪx=6���ó�M��2��2+b����N��6��6+b����CM=
��CN=6+b��MN=4
���ٵ�CM=CNʱ��42+��2+b��2=��6+b��2����ã�b=-2����ʱM��2��0�����ڵ�CM=MNʱ��42+��2+b��2=��4
��2����ã�b1=2��b1=-6������������ȥ������ʱM��2��4�����۵�CM=MNʱ��6+b=4
����ã�b=4
-6����ʱM��2��4
-4����
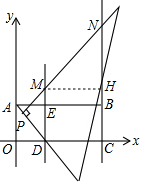
��3������������֤����PBN�ס�DEP���ó�BN��ֵ�����S��x֮��ĺ�����ϵʽ�����ݢٵ�0��x��2ʱ��S=x2-8x+12=��x-4��2-4���ڵ�2��x��6ʱ��S=-x2+8x-12=-��x-4��2+4�����ɵó��𰸣�
��2���ɷ��ۿ�֪�ı���AODEΪ�����Σ���M��MH��BC��H���������NMH=��MNH=45�㣬�ó�NH=MH=4��MN=4
| 2 |
| 42+(2+b)2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
��3������������֤����PBN�ס�DEP���ó�BN��ֵ�����S��x֮��ĺ�����ϵʽ�����ݢٵ�0��x��2ʱ��S=x2-8x+12=��x-4��2-4���ڵ�2��x��6ʱ��S=-x2+8x-12=-��x-4��2+4�����ɵó��𰸣�
����⣺��1���߽���AOD��AD���ۣ�ʹO������AB���ϵ�E�㴦��
���OAD=��EAD=45�㣬DE=OD��
��OA=OD��
��OA=2��
��OD=2��
��D�������ǣ�2��0����DE=OD=2��
��E�������ǣ�2��2����
�ʴ�Ϊ����2��0������2��2����
��2�����ڵ�Mʹ��CMNΪ���������Σ��������£�
�ɷ��ۿ�֪�ı���AODEΪ�����Σ�
��M��MH��BC��H��
�ߡ�PDM=��PMD=45�㣬���NMH=��MNH=45�㣬
NH=MH=4��MN=4
��
��ֱ��OE�Ľ���ʽΪ��y=x���������MN��OE��
����MN�Ľ���ʽΪy=x+b��
��DE�Ľ���ʽΪx=2��BC�Ľ���ʽΪx=6��
��M��2��2+b����N��6��6+b����
CM=
��CN=6+b��MN=4
��
������������ۣ�
�ٵ�CM=CNʱ��
42+��2+b��2=��6+b��2��
��ã�b=-2����ʱM��2��0����
�ڵ�CM=MNʱ��
42+��2+b��2=��4
��2��
��ã�b1=2��b2=-6������������ȥ����
��ʱM��2��4����
�۵�CN=MNʱ��
6+b=4
��
��ã�b=4
-6����ʱM��2��4
-4����
�������������ڵ�Mʹ��CMNΪ���������Σ�M�������Ϊ��
��2��0������2��4������2��4
-4����
��3����������ã�
��0��x��2ʱ��
�ߡ�BPN+��DPE=90�㣬
��BPN+��BNP=90�㣬
���DPE=��BNP��
�֡�PED=��NBP=90�㣬
���DEP�ס�PBN��
��
=
��
��
=
��
��BN=
��
��S��DBN=
•BN•BE
=
•
•4
�����ã�S=x2-8x+12��
��2��x��6ʱ��
�ߡ�PBN�ס�DEP��
��
=
��
��
=
��
��BN=
��
��S��DBN=
•BN•BE��
=
•
��4��
�����ã�S=-x2+8x-12��
��S��x֮��ĺ�����ϵʽ��
��
�ٵ�0��x��2ʱ��S=x2-8x+12=��x-4��2-4��
��x��4ʱ��S��x���������С����0��x��2��
�ڵ�2��x��6ʱ��S=-x2+8x-12=-��x-4��2+4��
��x��4ʱ��S��x���������С����4��x��6��
����������S��x�������Сʱ��0��x��2��4��x��6��
���OAD=��EAD=45�㣬DE=OD��
��OA=OD��
��OA=2��
��OD=2��
��D�������ǣ�2��0����DE=OD=2��
��E�������ǣ�2��2����
�ʴ�Ϊ����2��0������2��2����

��2�����ڵ�Mʹ��CMNΪ���������Σ��������£�
�ɷ��ۿ�֪�ı���AODEΪ�����Σ�
��M��MH��BC��H��
�ߡ�PDM=��PMD=45�㣬���NMH=��MNH=45�㣬
NH=MH=4��MN=4
| 2 |
��ֱ��OE�Ľ���ʽΪ��y=x���������MN��OE��
����MN�Ľ���ʽΪy=x+b��
��DE�Ľ���ʽΪx=2��BC�Ľ���ʽΪx=6��
��M��2��2+b����N��6��6+b����
CM=
| 42+(2+b)2 |
| 2 |
������������ۣ�
�ٵ�CM=CNʱ��
42+��2+b��2=��6+b��2��
��ã�b=-2����ʱM��2��0����
�ڵ�CM=MNʱ��
42+��2+b��2=��4
| 2 |
��ã�b1=2��b2=-6������������ȥ����
��ʱM��2��4����
�۵�CN=MNʱ��
6+b=4
| 2 |
��ã�b=4
| 2 |
| 2 |
�������������ڵ�Mʹ��CMNΪ���������Σ�M�������Ϊ��
��2��0������2��4������2��4
| 2 |
��3����������ã�
��0��x��2ʱ��
�ߡ�BPN+��DPE=90�㣬
��BPN+��BNP=90�㣬
���DPE=��BNP��
�֡�PED=��NBP=90�㣬
���DEP�ס�PBN��
��
| PB |
| DE |
| BN |
| EP |
��
| 6-x |
| 2 |
| BN |
| 2-x |
��BN=
| (2-x)(6-x) |
| 2 |
��S��DBN=
| 1 |
| 2 |
=
| 1 |
| 2 |
| (2-x)(6-x) |
| 2 |
�����ã�S=x2-8x+12��

��2��x��6ʱ��
�ߡ�PBN�ס�DEP��
��
| PB |
| NB |
| DE |
| PB |
��
| x-2 |
| NB |
| 2 |
| 6-x |
��BN=
| (x-2)(6-x) |
| 2 |
��S��DBN=
| 1 |
| 2 |
=
| 1 |
| 2 |
| (x-2)(6-x) |
| 2 |
�����ã�S=-x2+8x-12��
��S��x֮��ĺ�����ϵʽ��
|
�ٵ�0��x��2ʱ��S=x2-8x+12=��x-4��2-4��
��x��4ʱ��S��x���������С����0��x��2��
�ڵ�2��x��6ʱ��S=-x2+8x-12=-��x-4��2+4��
��x��4ʱ��S��x���������С����4��x��6��
����������S��x�������Сʱ��0��x��2��4��x��6��
���������⿼����һ�κ������ۺϣ��õ���֪ʶ���ǹ��ɶ�����һ�κ��������κ�����ͼ�������ʡ���ԳƵȣ��ؼ����ۺ������й�֪ʶ���������꣬��һ���ۺ��⣮

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��2013•���ݣ���ͼ��������ĸ���ͼ�ǣ�������
��2013•���ݣ���ͼ��������ĸ���ͼ�ǣ������� ��2013•���ݣ���ͼ��10����ͬ�ij�����ǽשƴ��һ�����Σ��賤����ǽש�ij��Ϳ��ֱ�Ϊx����y���ף����������з�������ȷ���ǣ�������
��2013•���ݣ���ͼ��10����ͬ�ij�����ǽשƴ��һ�����Σ��賤����ǽש�ij��Ϳ��ֱ�Ϊx����y���ף����������з�������ȷ���ǣ������� ��2013•���ݣ���ͼ��������ODBC�У�OC=1��OA=OB���������ϵ�A��ʾ������
��2013•���ݣ���ͼ��������ODBC�У�OC=1��OA=OB���������ϵ�A��ʾ������ ��2013•���ݣ���ͼ��һ����Ϊ2���Ŀ̶ȳߣ��̶ȵ�λ�����ף�������Բ�β������ı����ϣ��̶ȳߵ�һ���뱭���������У���һ���뱭�������������㴦�Ķ���ǡ����3��9����ô�������ı������ذ뾶Ϊ
��2013•���ݣ���ͼ��һ����Ϊ2���Ŀ̶ȳߣ��̶ȵ�λ�����ף�������Բ�β������ı����ϣ��̶ȳߵ�һ���뱭���������У���һ���뱭�������������㴦�Ķ���ǡ����3��9����ô�������ı������ذ뾶Ϊ