题目内容
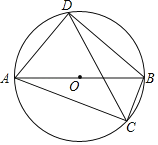
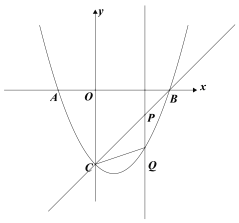
【题目】如图,抛物线y=![]() x2+mx+4m与x轴交于点A(
x2+mx+4m与x轴交于点A(![]() ,0)和点B(
,0)和点B(![]() ,0),与y轴交于点C,
,0),与y轴交于点C,![]() ,若对称轴在y轴的右侧.
,若对称轴在y轴的右侧.
(1)求抛物线的解析式
(2)在抛物线的对称轴上取一点M,使|MC-MB|的值最大;
(3)点Q是抛物线上任意一点,过点Q作PQ⊥x轴交直线BC于点P,连接CQ,当△CPQ是等腰三角形时,求点P的坐标.

【答案】(1)y=![]() -x-4;(2)M(1,-6);(3)P1 (
-x-4;(2)M(1,-6);(3)P1 (![]() ),P2(2,-2),P3(
),P2(2,-2),P3(![]() ).
).
【解析】
(1)利用根与系数的关系即可求出m,结合对称轴在y轴右侧可得结果;
(2)根据点A和点B关于对称轴对称,过点AC作直线交对称轴于点M,求出A,B,C的坐标,求出AC的表达式,得到点M的坐标即可;
(3)分PC=PQ,QC=QP,CP=CQ分别讨论,求出相应x值即可.
解:(1)∵y=![]() x2+mx+4m与x轴交于
x2+mx+4m与x轴交于![]() ,0)和点B(
,0)和点B(![]() ,0),
,0),
∴![]() 是方程
是方程![]() x2+mx+4m=0的两个根,
x2+mx+4m=0的两个根,
![]() ,
,
![]() ,
,
![]()
∴(-2m)2-16m=20,
解得m1=5,m2=-1,
∵对称轴在y轴的右侧,
∴m=-1,
∴y=![]() -x-4;
-x-4;
(2)y=![]() -x-4中,当x=0时,y=-4,
-x-4中,当x=0时,y=-4,
当y=0时![]() =-2,
=-2,![]() =4,
=4,
∴A(-2,0),B(4,0),C(0,-4),
过点AC作直线交对称轴于点M,
设直线AC的解析式为y=kx+b,
将(-2,0),(0,-4)代入,
则![]() ,
,
解得![]() ,
,
得y=-2x-4,当x=1时,y=-6,
∴M(1,-6);
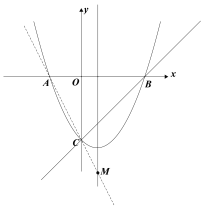
将(4,0),(0,-4)代入,
则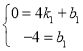 ,
,
解得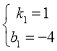 ,
,
得y=x-4,
∴∠OCB=∠OBC=45°,
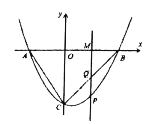
设P的横坐标为x,作PH⊥y轴于H,
则PC=![]() ,
,
∴PQ=|(x-4)-![]() -x-4)|
-x-4)|
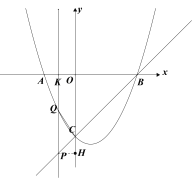
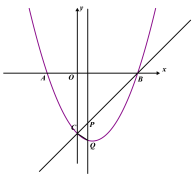
(图一) (图二)
如图一图二,当CQ=CP时,(x-4)+![]() -x-4)=-8,
-x-4)=-8,
x=0,不合题意,所以不存在;
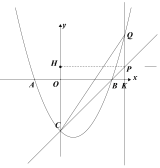
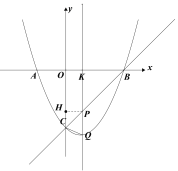
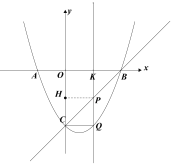
(图三) (图四) (图五)
如图三,当PC=PQ时,![]() =(x-4)-
=(x-4)- ![]() -x-4),
-x-4),
解得x=![]() ,
,
∴P(![]() )
)
如图四,当CQ=PQ时,x=(x-4)- ![]() -x-4),
-x-4),
解得x=2,
∴P(2,-2);
如图五,当PC=PQ时 ,
![]() -x-4)-(x-4)=
-x-4)-(x-4)=![]() ,
,
解得:x=![]() ,
,
∴P(![]() );
);
综上:P1(![]() ) ,P2(2,-2),P3(
) ,P2(2,-2),P3(![]() ).
).

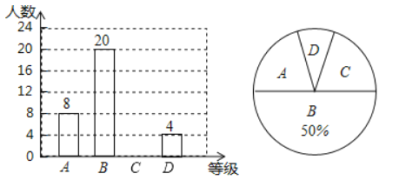
【题目】某校为了调查学生对卫生健康知识,特别是疫情防控下的卫生常识的了解,现从九年级![]() 名学生中随机抽取了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整).
名学生中随机抽取了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整).
组别 | 成绩 | 人数 |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
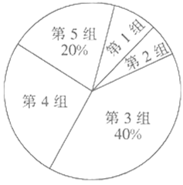
请结合图表信息完成下列各题.
(1)表中a的值为_____,b的值为______;在扇形统计图中,第![]() 组所在扇形的圆心角度数为______°;
组所在扇形的圆心角度数为______°;
(2)若测试成绩不低于![]() 分为优秀,请你估计从该校九年级学生中随机抽查一个学生,成绩为优秀的概率.
分为优秀,请你估计从该校九年级学生中随机抽查一个学生,成绩为优秀的概率.
(3)若测试成绩在![]() 分以上(含
分以上(含![]() 分)均为合格,其他为不合格,请你估计该校九年级学生中成绩不合格的有多少人.
分)均为合格,其他为不合格,请你估计该校九年级学生中成绩不合格的有多少人.