题目内容
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)= ![]() . 例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)=
. 例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)= ![]() .
.
(Ⅰ)如果一个正整数m是另外一个正整数n的平方,我们称正整数m是完全平方数.
求证:对任意一个完全平方数m,总有F(m)=1;
(Ⅱ)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数t为“吉祥数”,求所有“吉祥数”;
(Ⅲ)在(2)所得“吉祥数”中,求F(t)的最大值.
【答案】解:(Ⅰ)证明:对任意一个完全平方数m,设m=n2(n为正整数), ∵|n﹣n|=0,
∴n×n是m的最佳分解,
∴对任意一个完全平方数m,总有F(m)= ![]() =1;
=1;
(Ⅱ)设交换t的个位上数与十位上的数得到的新数为t′,则t′=10y+x,
∵t是“吉祥数”,
∴t′﹣t=(10y+x)﹣(10x+y)=9(y﹣x)=36,
∴y=x+4,
∵1≤x≤y≤9,x,y为自然数,
∴满足“吉祥数”的有:15,26,37,48,59;
(Ⅲ)F(15)= ![]() ,F(26)=
,F(26)= ![]() ,F(37)=
,F(37)= ![]() ,F(48)=
,F(48)= ![]() =
= ![]() ,F(59)=
,F(59)= ![]() ,
,
∵ ![]() >
> ![]() >
> ![]() >
> ![]() >
> ![]() ,
,
∴所有“吉祥数”中,F(t)的最大值为 ![]() .
.
【解析】(Ⅰ)对任意一个完全平方数m,设m=n2(n为正整数),找出m的最佳分解,确定出F(m)的值即可; (Ⅱ)设交换t的个位上数与十位上的数得到的新数为t′,则t′=10y+x,根据“吉祥数”的定义确定出x与y的关系式,进而求出所求即可;
(Ⅲ)利用“吉祥数”的定义分别求出各自的值,进而确定出F(t)的最大值即可.
【考点精析】掌握因式分解的应用是解答本题的根本,需要知道因式分解是整式乘法的逆向变形,可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案【题目】甲、乙两名队员参加射击训练,成绩被分别绘制成如下两个统计图:
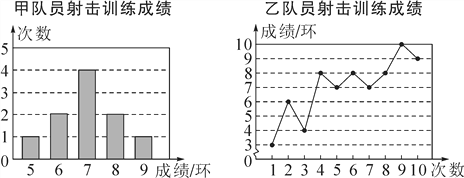
根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | 4.2 |
(1)则表格中a,b的值分别是a=________,b=________;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?