题目内容
【题目】如图,在矩形ABCD中,E,F分别是AD,BC的中点,连结AF,BE,CE,DF分别交于点M,N,则四边形EMFN是( )

A. 梯形B. 菱形
C. 矩形D. 无法确定
【答案】B
【解析】
求出四边形ABFE为平行四边形,四边形BFDE为平行四边形,根据平行四边形的性质得出BE∥FD,即ME∥FN,同理可证EN∥MF,得出四边形EMFN为平行四边形,求出ME=MF,根据菱形的判定得出即可.
连接EF.
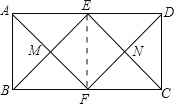
∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
又∵E,F分别为AD,BC中点,
∴AE∥BF,AE=BF,ED∥CF,DE=CF,
∴四边形ABFE为平行四边形,四边形BFDE为平行四边形,
∴BE∥FD,即ME∥FN,
同理可证EN∥MF,
∴四边形EMFN为平行四边形,
∵四边形ABFE为平行四边形,∠ABC为直角,
∴ABFE为矩形,
∴AF,BE互相平分于M点,
∴ME=MF,
∴四边形EMFN为菱形.
故选B.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
【题目】某学校计划组织全校1500名师生外出参加集体活动.经过研究,决定租用当地租车公司一共60辆![]() 、
、![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人 | 400元 |
| 20人 | 300元 |
注:载客量指的是每辆客车最多可载该校师生的人数.
学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过22000元,一共有几种租车方案?并结合函数性质说明哪种租车方案最省钱?