题目内容
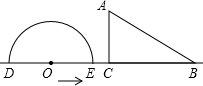
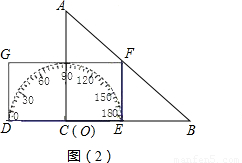
如图,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=10cm.点O以2cm/s的速度在直线BC上从左向右运动,设运动时间为t(s),当t=0s时,点O在△ABC的左侧,OC=5cm.以点O为圆心、 cm长度为半径r的半圆O与直线BC交于D、E两点
cm长度为半径r的半圆O与直线BC交于D、E两点
(1)当t为何值时,△ABC的一边所在直线与半圆O所在的圆相切?
(2)当△ABC的一边所在直线与半圆O所在的圆相切时,如果半圆O与直线DE围成的区域与△ABC三边围成的区域有重叠部分,求重叠部分的面积.

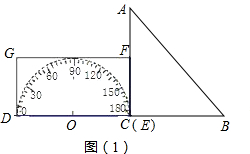
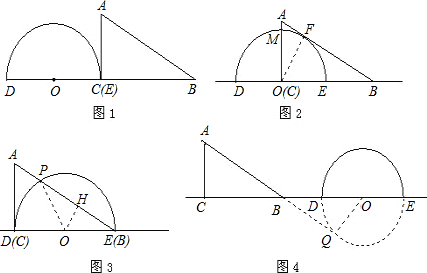
解:(1)①如图1,当点E与点C重合时,
∵AC⊥DE,OC=OE= cm,
cm,
∴AC与半圆O所在的圆相切,
∵原来OC=5,
∴点O运动了(5-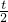 )cm,
)cm,
∵点O以2cm/s的速度在直线BC上从左向右运动,
∴运动时间为:t=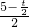 ,
,
t=2(秒),
∴当t=2时,△ABC的边AC所在直线与半圆O所在的圆相切,
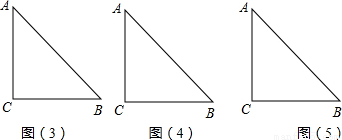
②如图2,经过t秒后,动圆圆心移动的为2t,而原来OB=OC+BC=15,此时动圆圆心到B的距离为(15-2t),
此时动圆圆心到AB的距离为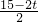 (30度角所对的直角边等于斜边的一半),
(30度角所对的直角边等于斜边的一半),
而此时圆的半径是 t,
t,
则可得: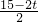 =
= t,
t,
解得:t=5.
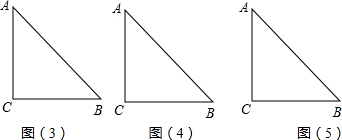
③如图3,当圆与AC相切时,2t-5= t,解得:t=
t,解得:t= 秒;
秒;
④如图4,当点O运动到B点的右侧,OB=2t-5-BC=2t-15,
∵在Rt△QOB中,∠OBQ=30°,
∴OQ= OB=
OB= (2t-15)=t-
(2t-15)=t-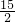 ,
,
圆O的半径是 t,则t-
t,则t-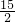 =
=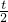 ,解得:t=15.
,解得:t=15.
总之,当t为2s,10s, s,15s时,△ABC的一边所在的直线与半圆O所在圆相切.
s,15s时,△ABC的一边所在的直线与半圆O所在圆相切.
(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有如图②与③所示的两种情形.
①如图②,设OA与半圆O的交点为M,易知重叠部分是圆心角为90°,半径为5cm的扇形,所求重叠部分面积为:S扇形EOM= π×52=
π×52=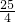 π(cm2)
π(cm2)
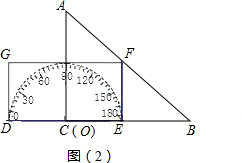
②图③,当圆O与AC相切时,半径长是 ×
× =
= ,
,
则半圆O在△ABC的内部,因而重合部分就是半圆O,则面积是: π(
π( )2=
)2=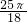 .
.
分析:(1)随着半圆的运动分四种情况:①当点E与点C重合时,AC与半圆相切,②当点O运动到点C时,AB与半圆相切,③当点O运动到BC的中点时,AC再次与半圆相切,④当点O运动到B点的右侧时,AB的延长线与半圆所在的圆相切.分别求得半圆的圆心移动的距离后,再求得运动的时间.
(2)在1中的②,③中半圆与三角形有重合部分.在②图中重叠部分是圆心角为90°,半径为6cm的扇形,故可根据扇形的面积公式求解.在③图中,所求重叠部分面积为=S△POB+S扇形DOP.
点评:本题利用了直线与圆相切的概念,扇形的面积公式,直角三角形的面积公式,锐角三角函数的概念求解.
∵AC⊥DE,OC=OE=
 cm,
cm,∴AC与半圆O所在的圆相切,
∵原来OC=5,
∴点O运动了(5-
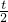 )cm,
)cm,∵点O以2cm/s的速度在直线BC上从左向右运动,
∴运动时间为:t=
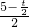 ,
,t=2(秒),
∴当t=2时,△ABC的边AC所在直线与半圆O所在的圆相切,
②如图2,经过t秒后,动圆圆心移动的为2t,而原来OB=OC+BC=15,此时动圆圆心到B的距离为(15-2t),
此时动圆圆心到AB的距离为
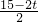 (30度角所对的直角边等于斜边的一半),
(30度角所对的直角边等于斜边的一半),而此时圆的半径是
 t,
t,则可得:
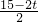 =
= t,
t,解得:t=5.
③如图3,当圆与AC相切时,2t-5=
 t,解得:t=
t,解得:t= 秒;
秒;④如图4,当点O运动到B点的右侧,OB=2t-5-BC=2t-15,
∵在Rt△QOB中,∠OBQ=30°,
∴OQ=
 OB=
OB= (2t-15)=t-
(2t-15)=t-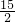 ,
,圆O的半径是
 t,则t-
t,则t-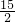 =
=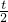 ,解得:t=15.
,解得:t=15.总之,当t为2s,10s,
 s,15s时,△ABC的一边所在的直线与半圆O所在圆相切.
s,15s时,△ABC的一边所在的直线与半圆O所在圆相切.
(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有如图②与③所示的两种情形.
①如图②,设OA与半圆O的交点为M,易知重叠部分是圆心角为90°,半径为5cm的扇形,所求重叠部分面积为:S扇形EOM=
 π×52=
π×52=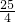 π(cm2)
π(cm2)②图③,当圆O与AC相切时,半径长是
 ×
× =
= ,
,则半圆O在△ABC的内部,因而重合部分就是半圆O,则面积是:
 π(
π( )2=
)2=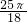 .
.分析:(1)随着半圆的运动分四种情况:①当点E与点C重合时,AC与半圆相切,②当点O运动到点C时,AB与半圆相切,③当点O运动到BC的中点时,AC再次与半圆相切,④当点O运动到B点的右侧时,AB的延长线与半圆所在的圆相切.分别求得半圆的圆心移动的距离后,再求得运动的时间.
(2)在1中的②,③中半圆与三角形有重合部分.在②图中重叠部分是圆心角为90°,半径为6cm的扇形,故可根据扇形的面积公式求解.在③图中,所求重叠部分面积为=S△POB+S扇形DOP.
点评:本题利用了直线与圆相切的概念,扇形的面积公式,直角三角形的面积公式,锐角三角函数的概念求解.

练习册系列答案
相关题目