题目内容
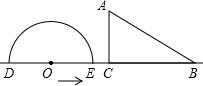
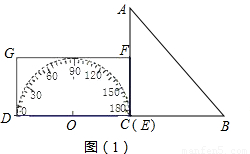
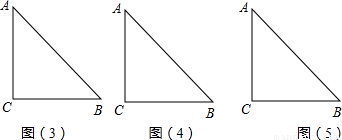
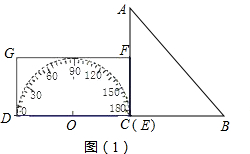
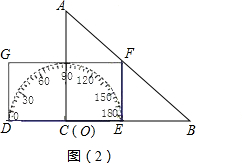
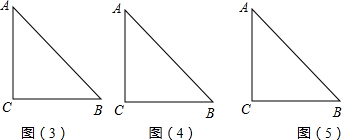
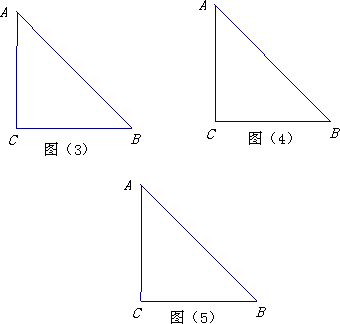
如图,形如三角板的△ABC中,∠ACB=90°,∠ABC=45°,BC=12cm,形如矩形量角器的半圆O的直径DE=12cm,矩形DEFG的宽EF=6cm,矩形量角器以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在BC所在的直线上,设运动时间为x(s),矩形量角器和△ABC的重叠部分的面积为S(cm2).当x=0(s)时,点E与点C重合.(图(3)、图(4)、图(5)供操作用).(1)当x=3时,如图(2),S=
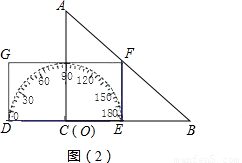
(2)当3<x<6时,求S关于x的函数关系式;
(3)当6<x<9时,求S关于x的函数关系式;
(4)当x为何值时,△ABC的斜边所在的直线与半圆O所在的圆相切?
分析:当3<x<6时,重叠部分是不规则的四边形,不能直接用x表示,要采用面积的分割法来求,先求S△ABC,S△AMN,再求S△BEH,然后求重叠部分的面积;当6<x<9时,重叠部分也是不规则的四边形,也采用面积的分割法来求,先求S△ABC,S△AHM,再
求S四边形HGDC,这样才能求出S与x的函数关系式
求S四边形HGDC,这样才能求出S与x的函数关系式
解答:解:(1)36,54,18(7分)
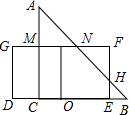
(2)如图,设矩形DEFG与斜边AB的交点分别为N、H,与直角边AC的交点为M;
∵BE=12-2x,AM=12-6=6,(4分)
∴S=S△ABC-S△AMN-S△BHE=
×12×12-
×6×6-
×(12-2x)2=-2x2+24x-18,
∴当3<x<6时,S=-2x2+24x-18.(6分)
(3)如图,
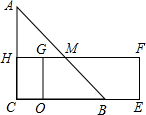
设矩形DEFG与斜边AB的交点为M,延长FG交AC于点H;
∵AH=12-6=6,HG=2x-12,(7分)
∴S=S△ABC-S△AHM-S矩形HCOG=
×12×12-
×6×6-6×(2x-12)=-12x+126,
∴当6<x<9时,S=-12x+126.(9分)
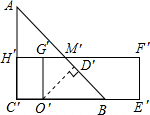
(4)如图,
①过点O′作O′D′⊥AB于点D′,由题意得O′D′=6;
∵∠ABC=45°,∠O′D′B=90°,
∴O′B=
=6
,
∴x1=
=9-3
(秒);(10分)
②过点O作OE⊥AB,交AB的延长线于点E,由题意得OE=6;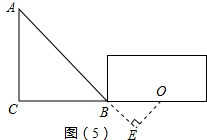
∵∠OBE=45°,∠OEB=90°,
∴OB=
=6
,
∴x2=
=9+3
,(秒)
故当x等于(9-3
)秒或(9+3
)秒时,△ABC的斜边所在的直线与半圆O所在的圆相切.(12分)

(2)如图,设矩形DEFG与斜边AB的交点分别为N、H,与直角边AC的交点为M;
∵BE=12-2x,AM=12-6=6,(4分)
∴S=S△ABC-S△AMN-S△BHE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当3<x<6时,S=-2x2+24x-18.(6分)
(3)如图,

设矩形DEFG与斜边AB的交点为M,延长FG交AC于点H;
∵AH=12-6=6,HG=2x-12,(7分)
∴S=S△ABC-S△AHM-S矩形HCOG=
| 1 |
| 2 |
| 1 |
| 2 |
∴当6<x<9时,S=-12x+126.(9分)

(4)如图,
①过点O′作O′D′⊥AB于点D′,由题意得O′D′=6;
∵∠ABC=45°,∠O′D′B=90°,
∴O′B=
| 62+62 |
| 2 |
∴x1=
6+12-6
| ||
| 2 |
| 2 |
②过点O作OE⊥AB,交AB的延长线于点E,由题意得OE=6;

∵∠OBE=45°,∠OEB=90°,
∴OB=
| 62+62 |
| 2 |
∴x2=
6+12+6
| ||
| 2 |
| 2 |
故当x等于(9-3
| 2 |
| 2 |
点评:此题用运动的知识,把求函数关系式与三角形的有关知识有机结合起来,综合性比较强.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
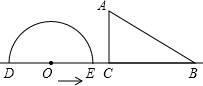

 cm长度为半径r的半圆O与直线BC交于D、E两点
cm长度为半径r的半圆O与直线BC交于D、E两点