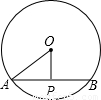
题目内容
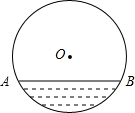 如图直径为26cm的圆柱形的油槽内装入一些油以后截面如图所示,若油面宽AB=24cm,求油的最大深度.
如图直径为26cm的圆柱形的油槽内装入一些油以后截面如图所示,若油面宽AB=24cm,求油的最大深度.
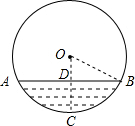 解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,
解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,∵AB=24cm,
∴BD=
 AB=
AB= ×24=12cm,
×24=12cm,∵⊙O的直径为26cm,
∴OB=OC=12cm,
在Rt△OBD中,OD=
 =
= =5cm,
=5cm,∴CD=OC-OD=13-5=8cm.
答;油的最大深度为8cm.
分析:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,先由垂径定理求出BD的长,再根据勾股定理求出OD的长,进而可得出CD的长.
点评:本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
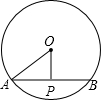 如图,⊙O的直径为26cm,弦AB长为24cm,且OP⊥AB于P点,则tan∠AOP的值为
如图,⊙O的直径为26cm,弦AB长为24cm,且OP⊥AB于P点,则tan∠AOP的值为