题目内容
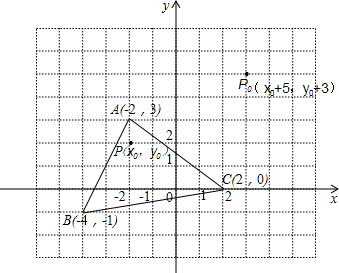
在平面直角坐标系x0y中,已知A(4,2),B(2,-2),以原点O为位似中心,按位似比1:2把△OAB缩小,则点A的对应点A′的坐标为
- A.(3,1)
- B.(-2,-1)
- C.(3,1)或(-3,-1)
- D.(2,1)或(-2,-1)
D
分析:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k,结合题意即可得出答案.
解答:∵A(4,2),B(2,-2)两点,以坐标原点O为位似中心,相似比为 ,
,
∴对应点A′的坐标分别是:A′(2,1)或(-2,-1).
故选D.
点评:此题主要考查了位似变换的性质,根据各点到位似中心的距离比也等于相似比是解决问题的关键.
分析:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k,结合题意即可得出答案.
解答:∵A(4,2),B(2,-2)两点,以坐标原点O为位似中心,相似比为
 ,
,∴对应点A′的坐标分别是:A′(2,1)或(-2,-1).
故选D.
点评:此题主要考查了位似变换的性质,根据各点到位似中心的距离比也等于相似比是解决问题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 (2012•鼓楼区二模)已知反比例函数y1=
(2012•鼓楼区二模)已知反比例函数y1=
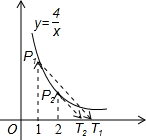 如图,在平面直角坐标系中,在x轴上代表初始值x0的那个点沿着竖线走,直到和曲线
如图,在平面直角坐标系中,在x轴上代表初始值x0的那个点沿着竖线走,直到和曲线