题目内容
【题目】如图,O是菱形ABCD对角线BD上的一点,且OC=OD,连接OA.
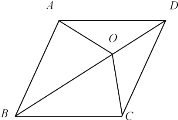
(1)求证:∠AOC=2∠ABC;
(2)求证:CD2=OD·BD.
【答案】(1)见解析;(2)见解析
【解析】
(1)连接AC,根据菱形的性质可知BD垂直平分AC,∠ADC=∠ABC,由中垂线的性质可得OA=OC,进而可得AO=OD,根据等腰三角形的性质可得∠BOC=2∠ODC,∠AOB=2∠ADO,进而根据菱形对角相等的性质即可得答案;(2)由菱形性质可得∠BDC=∠CBD,由(1)得∠ODC=∠OCD,可得∠OCD=∠CBD,由∠ODC是公共角,可证明△CDO∽△BDC,根据相似三角形的性质即可得答案.
(1)连接AC.
∵四边形ABCD是菱形,
∴BD垂直平分AC,∠ADC=∠ABC.
∵O是BD上一点,
∴OA=OC.
∵OC=OD,
∴AO=OD,∠ODC=∠OCD.
∴∠BOC=∠ODC+∠OCD=2∠ODC.
同理:∠AOB=2∠ADO,
∴∠AOC=2(∠ADO+∠ODC)=2∠ADC.
又∵∠ADC=∠ABC,
∴∠AOC=2∠ABC.
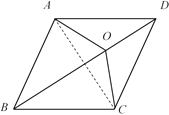
(2)∵四边形ABCD是菱形,
∴BC=CD.
∴∠BDC=∠CBD.
由(1)得∠ODC=∠OCD,
∴∠OCD=∠CBD.
在△CDO和△BDC中
∵∠ODC=∠CDB,∠OCD=∠CBD
∴△CDO∽△BDC.
∴![]() =
=![]() ,
,
即CD2=OD·BD.

【题目】为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,将测试成绩分成A、B、C、D四组,绘制了如下统计图表:
![]()
组别 | 分数/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
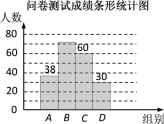
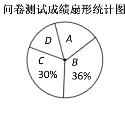
请结合以上信息解答下列问题:
(1)本次抽样调查的样本总量是多少?
(2)样本中,测试成绩在B组的频数是多少,在D组的频率是多少?
(3)样本中,这次测试成绩的中位数落在哪一组?
(4)如果该校共有800名学生,请估计成绩在90<x≤100的学生约有多少人?
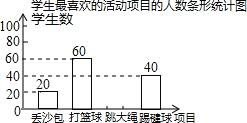
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息,解答下列问题
(1)m= ,n= ,p= .
(2)请根据以上信息直接补全条形统计图;
(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳学生最喜欢的活动项目的人数条形统计图.
【题目】中华文明,源远流长,中华汉字,寓意深广,为了传承优秀传统文化,某校九年级组织600名学生参加了一次“汉字听写”大赛![]() 赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:
赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:
90,92,81,82,78,95,86,88,72,66,62,68,89,86,93,97,100,73,76,80,77,81,86,89,82,85,71,68,74,98,90,97,100,84,87,73,65,92,96,60.
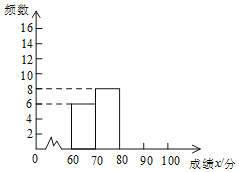
对上述成绩进行了整理,得到下列不完整的统计图表:
成绩 | 频数 | 频率 |
| 6 |
|
| 8 |
|
| a | b |
| c | d |
请根据所给信息,解答下列问题:
![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
![]() 请补全频数分布直方图;
请补全频数分布直方图;
![]() 若成绩在90分以上
若成绩在90分以上![]() 包括90分
包括90分![]() 的为“优”等,请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人?
的为“优”等,请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人?