题目内容
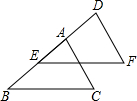 如图,AC=DF,BC=EF,AD=BE,∠BAC=80°,∠F=60°,则∠ABC等于
如图,AC=DF,BC=EF,AD=BE,∠BAC=80°,∠F=60°,则∠ABC等于
- A.80°
- B.60°
- C.40°
- D.20°
C
分析:根据AD=BE可得DE=AB,结合AC=DF,BC=EF,可以证明△BAC≌△EDF,即可得到∠B=∠DEF,∠BAC=∠EDF,∠C=∠F,由三角形内角和为180°,即可求出∠ABC的大小.
解答:∵AD=BE,
∴AD+AE=BE+AE,即DE=AB,
∵在△BAC和△EDF中,
 ,
,
∴△BAC≌△EDF(SSS),
∴∠B=∠DEF,∠BAC=∠EDF,∠C=∠F,
∵∠BAC=80°,∠F=60°,
∴∠ABC=180°-∠BAC-∠C=40°,
故选C.
点评:本题主要考查全等三角形的判定与性质的知识点,解答本题的关键是熟练掌握两三角形全等的判定定理,此题难度一般.
分析:根据AD=BE可得DE=AB,结合AC=DF,BC=EF,可以证明△BAC≌△EDF,即可得到∠B=∠DEF,∠BAC=∠EDF,∠C=∠F,由三角形内角和为180°,即可求出∠ABC的大小.
解答:∵AD=BE,
∴AD+AE=BE+AE,即DE=AB,
∵在△BAC和△EDF中,
 ,
,∴△BAC≌△EDF(SSS),
∴∠B=∠DEF,∠BAC=∠EDF,∠C=∠F,
∵∠BAC=80°,∠F=60°,
∴∠ABC=180°-∠BAC-∠C=40°,
故选C.
点评:本题主要考查全等三角形的判定与性质的知识点,解答本题的关键是熟练掌握两三角形全等的判定定理,此题难度一般.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 26、已知:如图,AC∥DF,∠A=∠F.
26、已知:如图,AC∥DF,∠A=∠F. 如图,AC=DF,AC∥DF,AE=DB.求证:BC=EF.
如图,AC=DF,AC∥DF,AE=DB.求证:BC=EF. 如图,AC=DF,∠ACB=∠DFE,点B、E、C在一条直线上,则下列条件中不能断定△ADC≌DEF的是( )
如图,AC=DF,∠ACB=∠DFE,点B、E、C在一条直线上,则下列条件中不能断定△ADC≌DEF的是( ) 如图:AC=DF,AD=BE,BC=EF.∠C=∠F吗?请说明理由.
如图:AC=DF,AD=BE,BC=EF.∠C=∠F吗?请说明理由. 如图,AC=DF,BC=EF,AD=BE,∠BAC=80°,∠F=60°,则∠ABC等于 ( )
如图,AC=DF,BC=EF,AD=BE,∠BAC=80°,∠F=60°,则∠ABC等于 ( )