��Ŀ����
����Ŀ����ֽƬ��ABC��DE�۵�ʹ��A����A�䴦��λ�ã�
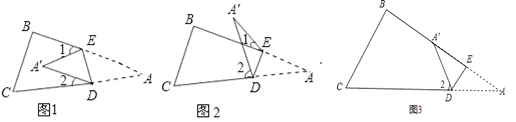
��1�����A�������ı���BCDE���ڲ�����ͼ1������A�����1+��2֮�����������������ϵ����˵�����ɣ�
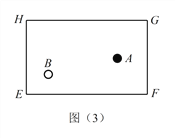
��2�����A�������ı���BCDE��BE���ϣ���ʱͼ1�еġ�1��Ϊ0��ǣ�����ͼ3�����A�����2֮��Ĺ�ϵ�� ��
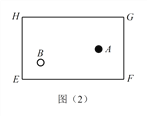
��3�����A�������ı���BCDE���ⲿ����ͼ2������ʱ��A�����1����2֮���ִ���������������ϵ����˵�����ɣ�
���𰸡���1��2��A=��1+��2����2��2��A=��2����3��2��A=��2-��1��
��������
�����������1�������۵����ʵó���AED=��A��ED����ADE=��A��DE�������������ڽǺͶ����ó���AED+��ADE=180��-��A��������1+��2=180��+180��-2����AED+��ADE��������ɣ�
��2������������������ʵó���DME=��A��+��1����2=��A+��DME�����뼴������𰸣�
�����������1��ͼ1�У�2��A=��1+��2��
�����ǣ�����DE�۵�A��A���غϣ�
���AED=��A��ED����ADE=��A��DE��
�ߡ�AED+��ADE=180��-��A����1+��2=180��+180��-2����AED+��ADE����
���1+��2=360��-2��180��-��A��=2��A��
��2��2��A=��2����ͼ
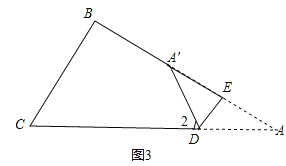
��2=��A+��EA��D=2��A��
��3����ͼ2��2��A=��2-��1��
�����ǣ�����DE�۵�A��A���غϣ�
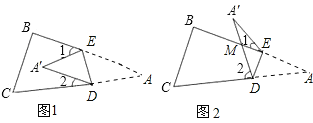
���A=��A����
�ߡ�DME=��A��+��1����2=��A+��DME��
���2=��A+��A��+��1��
��2��A=��2-��1��
����:1.�������ڽǺͶ�����2.�����ε�������ʣ�