题目内容
【题目】如图,在正方形ABCD中,点E、G分别是边AD、BC的中点,AF= ![]() AB.
AB.
(1)求证:EF⊥AG;
(2)若点F、G分别在射线AB、BC上同时向右、向上运动,点G运动速度是点F运动速度的2倍,EF⊥AG是否成立(只写结果,不需说明理由)?
(3)正方形ABCD的边长为4,P是正方形ABCD内一点,当S△PAB=S△OAB , 求△PAB周长的最小值.
【答案】
(1)
证明:∵四边形ABCD是正方形,
∴AD=AB,∠EAF=∠ABG=90°,
∵点E、G分别是边AD、BC的中点,AF= ![]() AB.
AB.
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴△AEF∽△BAG,
∴∠AEF=∠BAG,
∵∠BAG+∠EAO=90°,
∴∠AEF+∠EAO=90°,
∴∠AOE=90°,
∴EF⊥AG;
(2)
解:成立;理由如下:
根据题意得: ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]() ,
,
又∵∠EAF=∠ABG,
∴△AEF∽△BAG,
∴∠AEF=∠BAG,
∵∠BAG+∠EAO=90°,
∴∠AEF+∠EAO=90°,
∴∠AOE=90°,
∴EF⊥AG
(3)
解:过O作MN∥AB,交AD于M,BC于N,如图所示:
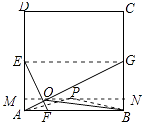
则MN⊥AD,MN=AB=4,
∵P是正方形ABCD内一点,当S△PAB=S△OAB,
∴点P在线段MN上,当P为MN的中点时,△PAB的周长最小,
此时PA=PB,PM= ![]() MN=2,
MN=2,
连接EG、PA、PB,则EG∥AB,EG=AB=4,
∴△AOF∽△GOE,
∴ ![]() =
= ![]() ,
,
∵MN∥AB,
∴ ![]() =
= ![]() ,
,
∴AM= ![]() AE=
AE= ![]() ×2=
×2= ![]() ,
,
由勾股定理得:PA= ![]() =
= ![]() ,
,
∴△PAB周长的最小值=2PA+AB= ![]() +4.
+4.
【解析】(1)由正方形的性质得出AD=AB,∠EAF=∠ABG=90°,证出 ![]() ,得出△AEF∽△BAG,由相似三角形的性质得出∠AEF=∠BAG,再由角的互余关系和三角形内角和定理证出∠AOE=90°即可;(2)证明△AEF∽△BAG,得出∠AEF=∠BAG,再由角的互余关系和三角形内角和定理即可得出结论;(3)过O作MN∥AB,交AD于M,BC于N,则MN⊥AD,MN=AB=4,由三角形面积关系得出点P在线段MN上,当P为MN的中点时,△PAB的周长最小,此时PA=PB,PM=
,得出△AEF∽△BAG,由相似三角形的性质得出∠AEF=∠BAG,再由角的互余关系和三角形内角和定理证出∠AOE=90°即可;(2)证明△AEF∽△BAG,得出∠AEF=∠BAG,再由角的互余关系和三角形内角和定理即可得出结论;(3)过O作MN∥AB,交AD于M,BC于N,则MN⊥AD,MN=AB=4,由三角形面积关系得出点P在线段MN上,当P为MN的中点时,△PAB的周长最小,此时PA=PB,PM= ![]() MN=2,连接EG,则EG∥AB,EG=AB=4,证明△AOF∽△GOE,得出
MN=2,连接EG,则EG∥AB,EG=AB=4,证明△AOF∽△GOE,得出 ![]() =
= ![]() ,证出
,证出 ![]() =
= ![]() ,得出AM=
,得出AM= ![]() AE=
AE= ![]() ,由勾股定理求出PA,即可得出答案.
,由勾股定理求出PA,即可得出答案.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.

 考前必练系列答案
考前必练系列答案【题目】某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表.
身高分组 | 频数 | 频率 |
152≤x<155 | 3 | 0.06 |
155≤x<158 | 7 | 0.14 |
158≤x<161 | m | 0.28 |
161≤x<164 | 13 | n |
164≤x<167 | 9 | 0.18 |
167≤x<170 | 3 | 0.06 |
170≤x<173 | 1 | 0.02 |

根据以上统计图表完成下列问题:
(1)统计表中m= , n= , 并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在:范围内;
(3)在身高≥167cm的4人中,甲、乙两班各有2人,现从4人中随机推选2人补充到学校国旗护卫队中,请用列表或画树状图的方法求出这两人都来自相同班级的概率.
【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | 1 |

根据图表提供的信息,解答下列问题:
(1)八年级一班有多少名学生?
(2)请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.










