题目内容
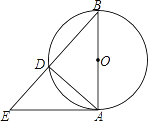
【题目】如图，AB为⊙O的直径，AE为⊙O的切线，若tan∠ABE= 
，AE=3，求BD的长．
【答案】BD= 
．
【解析】
由AB为⊙O的直径，得到∠ADB=90°，根据邻补角的定义得到∠ADE=90°，根据切线的性质得到∠EAB=90°，推出△EAD∽△EBA，根据相似三角形的性质得到
，得到AE2=EDEB，根据三角函数的定义得到AB=6，由勾股定理得到BE=
，即可得到结论．
∵AB为⊙O的直径， ∴∠ADB=90°，∴∠ADE=90°，
∵AE为⊙O的切线，
∴∠EAB=90°，
∵∠E=∠E，
∴△EAD∽△EBA，
∴，
∴AE2=EDEB，
在Rt△AEB中，AE=3，tan∠ABE=
，
∴
，
∴AB=6，
∴BE=
∴32=ED3
，
∴ED=
，
∴BD=BE﹣ED=3﹣=．
练习册系列答案
小学课时特训系列答案
相关题目
【题目】某学校20名数学教师的年龄（单位：岁）情况如下：29，42，58，37，53，52，49，24，37，46，42，55，40，38，50，26，54，26，44，52．
(1)填写下面的频率分布表：
分组 | 频数 | 频率 |
19.5～29.5 | ||
29.5～39.5 | ||
39.5～49.5 | ||
49.5～59.5 | ||
合计 |
(2)画出数据的频数分布直方图．
