题目内容
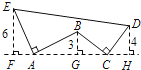
【题目】如图,射线OA∥射线CB,∠C=∠OAB=100°.点D、E在线段CB上,且∠DOB=∠BOA,OE平分∠DOC.
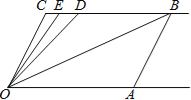
(1)试说明AB∥OC的理由;
(2)试求∠BOE的度数;
(3)平移线段AB;
①试问∠OBC:∠ODC的值是否会发生变化?若不会,请求出这个比值;若会,请找出相应变化规律.
②若在平移过程中存在某种情况使得∠OEC=∠OBA,试求此时∠OEC的度数.
【答案】(1)理由见解析(2)40°(3)①1:2②60°
【解析】试题分析:(1)根据OA//CB,得出![]() ,再根据已知条件,即可证明∠C+∠ABC=180°,从而得证.(2)根据两直线平行,同旁内角互补求出∠AOC,再求出∠EOB=
,再根据已知条件,即可证明∠C+∠ABC=180°,从而得证.(2)根据两直线平行,同旁内角互补求出∠AOC,再求出∠EOB=![]() ∠AOC.(3)①根据两直线平行,内错角相等可得∠AOB=∠OBC,再根据三角形的外角性质∠OEC=2∠OBC即可.②根据三角形的内角定理,求出∠COE=∠AOB,从而得到OB、OD、OE是∠AOC的四等分线,在利用三角形的内角定理即可求出∠OEC的度数.
∠AOC.(3)①根据两直线平行,内错角相等可得∠AOB=∠OBC,再根据三角形的外角性质∠OEC=2∠OBC即可.②根据三角形的内角定理,求出∠COE=∠AOB,从而得到OB、OD、OE是∠AOC的四等分线,在利用三角形的内角定理即可求出∠OEC的度数.
试题解析:(1)∵OA∥CB,∴∠OAB+∠ABC=180°,∵∠C=∠OAB=100°,∴∠C+∠ABC=180°,
∴AB∥OC . (2)∵CB∥OA,∴∠AOC=180°﹣∠C=180°﹣100°=80°,∵OE平分∠COD,∴∠COE=∠EOD,∵∠DOB=∠AOB,∴∠EOB=∠EOD+∠DOB=![]() ∠AOC=
∠AOC=![]() ×80°=40°;(3)①∵CB∥OA,∴∠AOB=∠OBC,∵∠EOB=∠AOB,∴∠EOB=∠OBC,∴∠OEC=∠EOB+∠OBC=2∠OBC,∴∠OBC:∠OEC=1:2,是定值;
×80°=40°;(3)①∵CB∥OA,∴∠AOB=∠OBC,∵∠EOB=∠AOB,∴∠EOB=∠OBC,∴∠OEC=∠EOB+∠OBC=2∠OBC,∴∠OBC:∠OEC=1:2,是定值;
②在△COE和△AOB中,∵∠OEC=∠OBA,∠C=∠OAB,∴∠COE=∠AOB,∴OB、OD、OE是∠AOC的四等分线,
∴∠COE=![]() ∠AOC=
∠AOC=![]() ×80°=20°,∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,∴∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
×80°=20°,∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,∴∠OEC=∠OBA,此时∠OEC=∠OBA=60°.

【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字49个.随机抽取了部分学生的听写结果,绘制成如下的图表.
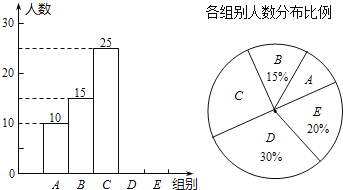
组别 | 正确字数x | 人数 |
A | 0≤x<10 | 10 |
B | 10≤x<20 | 15 |
C | 20≤x<30 | 25 |
D | 30≤x<40 | m |
E | 40≤x<50 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)求扇形统计图中“C组”所对应的圆心角的度数;
(3)已知该校共有2400名学生,如果听写正确的汉字的个数少于30个定为不合格,请你估计该校本次听写比赛不合格的学生人数.