题目内容
【题目】如图所示的数表是由1开始的连续自然数排列而成的，根据你观察的规律完成下面问题：
（1）第8行最后一个数是________；第n行共有__________个数，这行第一个数是__________，这行最后一个数是______________.
（2）求第10行各数的和.
【答案】（1）64、（2n-1)、 (n-1)2+1 、n2 ；（2）1729.
【解析】
（1）数为自然数，每行数的个数为1，3，5，…的奇数列；每行最后一个数为完全平方数，第n行最后一个数为n2.则第8行最后一个数是82；第n行共有（2n-1）个数；
第n行第一个数为(n-1)2+1；最后一个数为n2.
（2）由（1）可知第10行的第一个数是第9行最后一个数的下一个自然数，即92+1=82，最后一个数为102，求和即可.
（1） 64、（2n-1)、 (n-1)2+1 、n2
（2）82+83+84+…+98+99+100
=(82+100)+(83+99)+(84+98)+…+91
=91×2+91×2+91×2+…+91
=91×18+91
=91×19
=1729
【题目】阅读下面材料：
小明想探究函数
的性质，他借助计算器求出了y与x的几组对应值，并在平面直角坐标系中画出了函数图象：
x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
y | … | 2.83 | 1.73 | 0 | 0 | 1.73 | 2.83 | … |
小聪看了一眼就说：“你画的图象肯定是错误的．”
请回答：小聪判断的理由是_____________．请写出函数的一条性质：_____________．
【题目】在一次社会调查活动中，小华收集到某“健步走运动”团队中20名成员一天行走的步数，记录如下： 5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组，并统计整理，绘制了如下尚不完整的统计图表：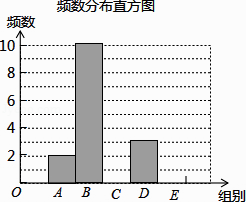
步数分组统计表
组别 | 步数分组 | 频数 |
A | 5500≤x＜6500 | 2 |
B | 6500≤x＜7500 | 10 |
C | 7500≤x＜8500 | m |
D | 8500≤x＜9500 | 3 |
E | 9500≤x＜10500 | n |
请根据以上信息解答下列问题：
（1）求m，n的值；
（2）补全频数发布直方图；
（3）这20名“健步走运动”团队成员一天行走步数的中位数落在哪一组？
（4）若该团队共有120人，请估计其中一天行走步数不少于7500步的人数．
