题目内容
【题目】如图,直线AB,CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.
(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE=120°,求∠BOD的度数.
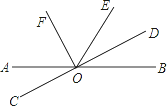
【答案】(1)与∠AOD互补的角有∠AOC,∠BOD,∠DOE;
(2)∠BOD =30°.
【解析】试题分析:(1)根据邻补角的定义确定出∠AOC和∠BOD,再根据角平分线的定义可得∠AOF=∠EOF,根据垂直的定义可得∠COF=∠DOF=90°,然后根据等角的余角相等求出∠DOE=∠ACO,从而最后得解;
(2)根据角平分线的定义求出∠AOF,再根据余角的定义求出∠AOC,然后根据对顶角相等解答.
试题解析:(1)∵直线AB,CD相交于点O,
∴∠AOC和∠BOD与∠AOD互补,
∵OF平分∠AOE,
∴∠AOF=∠EOF,
∵OF⊥CD,
∴∠COF=∠DOF=90°,
∴∠DOE=∠ACO,
∴∠DOE也是∠AOD的补角,
∴与∠AOD互补的角有∠AOC,∠BOD,∠DOE;
(2)∵OF平分∠AOE,
∴∠AOF=![]() ∠AOE=60°,
∠AOE=60°,
∵OF⊥CD,
∴∠COF=90°,
∴∠AOC=∠COF﹣∠AOF=90°﹣60°=30°,
∵∠AOC与∠BOD是对顶角,
∴∠BOD=∠AOC=30°.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目