题目内容
【题目】如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
①AM=AD+MC;②AM=DE+BM;③DE2=ADCM;④点N为△ABM的外心.其中正确的个数为( )
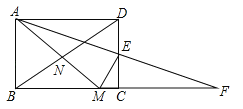
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】解:∵E为CD边的中点,∴DE=CE,又∵∠D=∠ECF=90°,∠AED=∠FEC,∴△ADE≌△FCE,∴AD=CF,AE=FE,又∵ME⊥AF,∴ME垂直平分AF,∴AM=MF=MC+CF,∴AM=MC+AD,故①正确;
当AB=BC时,即四边形ABCD为正方形时,设DE=EC=1,BM=a,则AB=2,BF=4,AM=FM=4﹣a,在Rt△ABM中,22+a2=(4﹣a)2,解得a=1.5,即BM=1.5,∴由勾股定理可得AM=2.5,∴DE+BM=2.5=AM,又∵AB<BC,∴AM=DE+BM不成立,故②错误;
∵ME⊥FF,EC⊥MF,∴EC2=CM×CF,又∵EC=DE,AD=CF,∴DE2=ADCM,故③正确;
∵∠ABM=90°,∴AM是△ABM的外接圆的直径,∵BM<AD,∴当BM∥AD时, ![]() <1,∴N不是AM的中点,∴点N不是△ABM的外心,故④错误.
<1,∴N不是AM的中点,∴点N不是△ABM的外心,故④错误.
综上所述,正确的结论有2个,故选B.

练习册系列答案
相关题目



