题目内容
(2012•闸北区二模)如图,在等腰△ABC中,AB=AC=10cm,cosB=
,点G是△ABC的重心.动点E从点A出发沿着射线AG以每秒1cm的速度移动,动点F从点C出发沿着射线CA以每秒2cm的速度移动,点E和点F同时出发,设它们的运动时间为t(秒).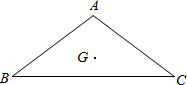
(1)求点A到点G的距离;
(2)在移动过程中,是否存在以点G为圆心GE长为半径的圆与以点C为圆心CF长为半径的圆外切?若存在,求出t值;若不存在,请说明理由;
(3)连接EF,在运动过程中,是否存在△AEF是等腰三角形?若存在,求出t值;若不存在,请说明理由.
| 4 | 5 |

(1)求点A到点G的距离;
(2)在移动过程中,是否存在以点G为圆心GE长为半径的圆与以点C为圆心CF长为半径的圆外切?若存在,求出t值;若不存在,请说明理由;
(3)连接EF,在运动过程中,是否存在△AEF是等腰三角形?若存在,求出t值;若不存在,请说明理由.
分析:(1)连接AG并延长,交边BC于点H.根据G是重心得到AH平分边BC,再根据AB=AC得到AH⊥BC,然后解直角三角形ABH即可求解;
(2)由(1)得:GH=2,HC=BH=8,根据两圆相外切两圆的圆心距等于两圆半径的和列出有关t的方程求得t的值即可;
(3)分当点F在边AC上时和当点F在CA的延长线上时两种情况利用等腰三角形的性质列出有关t的方程求得t的值即可求解.
(2)由(1)得:GH=2,HC=BH=8,根据两圆相外切两圆的圆心距等于两圆半径的和列出有关t的方程求得t的值即可;
(3)分当点F在边AC上时和当点F在CA的延长线上时两种情况利用等腰三角形的性质列出有关t的方程求得t的值即可求解.
解答:解:(1)连接AG并延长,交边BC于点H.
∵G是重心,
∴AH平分边BC,AG=
AH,
∵AB=AC
∴AH⊥BC.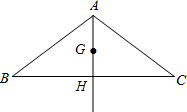
在Rt△ABH中,cosB=
,
即
=
,
∴BH=8,
∴AH=6,
∴AG=4.
(2)由(1)得:GH=2,HC=BH=8.
根据题意得:EG=|4-t|,CF=2t
∴rG=|4-t|,rC=2t
且圆心距CG=
=
=2
.
当圆G与圆C外切时:rG+rC=CG,
∴|4-t|+2t=2
,…(3分)
即:4-t+2t=2
(t<4)或t-4+2t=2
(t>4)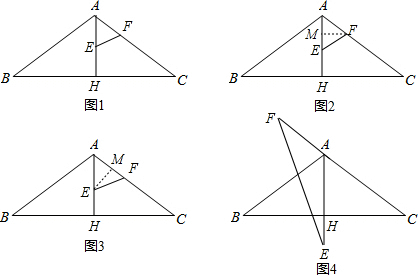
∴t1=2
-4(舍),t2=
即当t=
时两圆外切.
(3)•当点F在边AC上时:
①如图1,当AE=AF时,t=10-2t,∴t1=
.…(1分)
②如图2,当AF=EF时,过F作MF⊥AH于点M,
由MF∥HC,∴
=
,∴
=
,
∴t2=
.…(1分)
③如图3,当AE=EF时:过点E作EM⊥AC于点M,
易证△AEM∽△ACH,∴AM:AE=AH:AC,
∴
(10-2t):t=3:5,∴t3=
.…(1分)
•当点F在CA的延长线上时:
④如图4,只有AE=AF时,△AEF为等腰三角形,
∴t=2t-10,
∴t4=10.…(1分)
综上所述,当t=
、
、
、10的时候,△AEF是等腰三角形.
∵G是重心,
∴AH平分边BC,AG=
| 2 |
| 3 |
∵AB=AC
∴AH⊥BC.

在Rt△ABH中,cosB=
| BH |
| AB |
即
| BH |
| 10 |
| 4 |
| 5 |
∴BH=8,
∴AH=6,
∴AG=4.
(2)由(1)得:GH=2,HC=BH=8.
根据题意得:EG=|4-t|,CF=2t
∴rG=|4-t|,rC=2t
且圆心距CG=
| 22+82 |
| 68 |
| 17 |
当圆G与圆C外切时:rG+rC=CG,
∴|4-t|+2t=2
| 17 |
即:4-t+2t=2
| 17 |
| 17 |

∴t1=2
| 17 |
2
| ||
| 3 |
即当t=
2
| ||
| 3 |
(3)•当点F在边AC上时:
①如图1,当AE=AF时,t=10-2t,∴t1=
| 10 |
| 3 |
②如图2,当AF=EF时,过F作MF⊥AH于点M,
由MF∥HC,∴
| AM |
| AF |
| AH |
| AC |
| ||
| 10-2t |
| 3 |
| 5 |
∴t2=
| 60 |
| 17 |
③如图3,当AE=EF时:过点E作EM⊥AC于点M,
易证△AEM∽△ACH,∴AM:AE=AH:AC,
∴
| 1 |
| 2 |
| 25 |
| 8 |
•当点F在CA的延长线上时:
④如图4,只有AE=AF时,△AEF为等腰三角形,
∴t=2t-10,
∴t4=10.…(1分)
综上所述,当t=
| 10 |
| 3 |
| 25 |
| 8 |
| 60 |
| 17 |
点评:本题考查了相似形的综合知识,特别是第(3)题中利用了分类讨论的数学思想,这也是中考中常常考查的重点知识之一.

练习册系列答案
相关题目
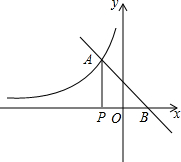 (2012•闸北区二模)已知:如图,一次函数y=kx+b的图象与反比例函数y=-
(2012•闸北区二模)已知:如图,一次函数y=kx+b的图象与反比例函数y=-