题目内容
 (2012•闸北区二模)已知:如图,一次函数y=kx+b的图象与反比例函数y=-
(2012•闸北区二模)已知:如图,一次函数y=kx+b的图象与反比例函数y=-| 2 | x |
(1)求点B的坐标及一次函数的解析式;
(2)设点C是x轴上的一个点,如果∠ACO=∠BAO,求出点C的坐标.
分析:(1)首先把A(-1,m)代入y=-
,即可求得m的值,又由S△ABP=2,则可求得点B的坐标,然后利用待定系数法即可求得此一次函数的解析式;
(2)由(1)可求得OA=
,AB=2
,分别从当点C在x轴的正半轴上与当点C在x轴的负半轴上时去分析,利用相似三角形的对应边成比例,即可求得答案.
| 2 |
| x |
(2)由(1)可求得OA=
| 5 |
| 2 |
解答:解:(1)把A(-1,m)代入y=-
,
得m=-
=2,
即点A的坐标为:(-1,2),
又∵S△ABP=
PB•AP,
∴2=
PB×2,
∴PB=2,
∴点B(1,0);
设直线AB的解析式为y=kx+b(k≠0),
把点A、B的坐标代入得:
,
解得:
,
故直线AB的解析式为y=-x+1;
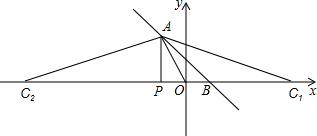 (2)∵点A(-1,2)、B(1,0),
(2)∵点A(-1,2)、B(1,0),
∴OA=
,AB=2
.如图:
当点C在x轴的正半轴上时,
∵∠ACO=∠BAO,∠AOC=∠BOA,
∴△OAC∽△OBA,
∴
=
,
∴
=
,
∴OC=5,
即点C1(5,0);
当点C在x轴的负半轴上时,
∵∠ACO=∠BAO,∠ABC=∠OBA,
∴△ABO∽△CBA,
∴
=
,
∴
=
,
∴CB=8,
即点C2(-7,0).
综上,点C的坐标为:(5,0),(-7,0).
| 2 |
| x |
得m=-
| 2 |
| -1 |
即点A的坐标为:(-1,2),
又∵S△ABP=
| 1 |
| 2 |
∴2=
| 1 |
| 2 |
∴PB=2,
∴点B(1,0);
设直线AB的解析式为y=kx+b(k≠0),
把点A、B的坐标代入得:
|
解得:
|
故直线AB的解析式为y=-x+1;
 (2)∵点A(-1,2)、B(1,0),
(2)∵点A(-1,2)、B(1,0),∴OA=
| 5 |
| 2 |
当点C在x轴的正半轴上时,
∵∠ACO=∠BAO,∠AOC=∠BOA,
∴△OAC∽△OBA,
∴
| OA |
| OC |
| OB |
| OA |
∴
| ||
| OC |
| 1 | ||
|
∴OC=5,
即点C1(5,0);
当点C在x轴的负半轴上时,
∵∠ACO=∠BAO,∠ABC=∠OBA,
∴△ABO∽△CBA,
∴
| AB |
| CB |
| OB |
| AB |
∴
| ||
| CB |
| 1 | ||
|
∴CB=8,
即点C2(-7,0).
综上,点C的坐标为:(5,0),(-7,0).
点评:此题考查了待定系数法求一次函数的解析式、相似三角形的判定与性质、反比例函数与一次函数的交点问题以及三角形面积问题.此题难度较大,注意掌握方程思想、分类讨论思想与数形结合思想的应用.

练习册系列答案
相关题目
