题目内容
【题目】在△ABC中,AB=AC=4,∠BAC=30°,以AC为一边作等边△ACD,连接BD.请画出图形,并直接写出△BCD的面积.
【答案】4![]() -4.
-4.
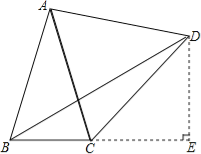
【解析】试题分析:首先根据题意画出图形,然后把BC边上的高作出来,过点D作DE⊥BC交BC的延长线于点E,利用勾股定理以及锐角三角函数求出BC,DE的长,进而求出△BCD的面积.
试题解析:首先根据题意画出图形,如图,由题意可知AB=AC=4,∠BAC=30°,△ACD是等边三角形,则AB=AD=DC=AC=4,∠BAD=∠BAC+∠CAD=30°+60°=90°,∠ABC=∠ACB=(180°-30°)÷2=75°,∴△ABD是等腰直角三角形,∴∠ABD=∠ADB=45°,∠DBE=75°-45°=30°,∠DCE=180°-60°-75°=45°,则△DCE是等腰直角三角形,CE=DE,∵DC=4,∴DE=EC=![]() =
=![]() ,∴BD=2DE=
,∴BD=2DE=![]() ,∴BE=BDcos30°=
,∴BE=BDcos30°=![]() ×
×![]() =
=![]() ,∴BC=BE﹣EC=2
,∴BC=BE﹣EC=2![]() ﹣2
﹣2![]() ,∴△BCD的面积为:
,∴△BCD的面积为: ![]() ×2
×2![]() ×(2
×(2![]() ﹣2
﹣2![]() )=4
)=4![]() ﹣4.
﹣4.

练习册系列答案
相关题目