题目内容
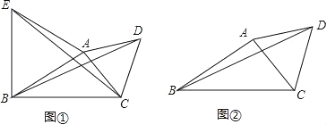
【题目】(1)如图①,△ABE,△ACD都是等边三角形,若CE=6,则BD的长=__;
(2)如图②,△ABC中,∠ABC=30°,AB=3,BC=4,D是△ABC外一点,且△ACD是等边三角形,则BD的长=__.
【答案】 6 5
【解析】试题分析:
(1)根据等边三角形的性质得到AE=AB,AD=AC,∠EAB=∠DAC=60°,则∠BAD=∠EAC,再根据三角形全等的判定方法可证得△ACE≌△ADB,根据全等的性质得出BD=CE即可;
(2)作等边三角形ABE,连接AE,则AE=AB=3,∠ABE=60°,证出∠CBE=90°,由勾股定理求出CE,即可得到结果.
试题解析:
(1)∵△ABE和△ACD是等边三角形,
∴BE=AE=AB=3,AD=AC,∠ABE=∠EAB=∠DAC=60°,
∴∠EAB+∠BAC=∠DAC+∠CAB,
∴∠BAD=∠EAC,
在△ACE和△ADB中, 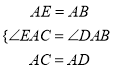 ,
,
∴△ACE≌△ADB(SAS),
∴BD=CE=6;
故答案为:6;
(2)作等边三角形ABE,连接AE,如图所示:

则AE=AB=3,∠ABE=60°,
∵∠ABC=30°,
∴∠CBE=∠ABE+∠ABC=90°,
∴CE=![]() ,
,
由(1)得:BD=CE=5;
故答案为:5.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目