��Ŀ����
����Ŀ�����Ķ����в���,Ȼ�������⣮
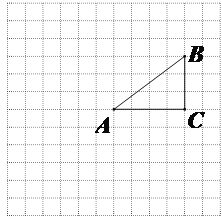
���ϣ���������![]() ���ǵ���������
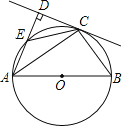
���ǵ���������![]() һ����������һ��������Ա��ཻ,�����뽻��֮����߶ΰ���������ηָ������С������,����ֵõ�����С��������һ��Ϊ����������,��һ����ԭ����������,���ǰ������߶ν�����������ε������ָ��ߣ�
һ����������һ��������Ա��ཻ,�����뽻��֮����߶ΰ���������ηָ������С������,����ֵõ�����С��������һ��Ϊ����������,��һ����ԭ����������,���ǰ������߶ν�����������ε������ָ��ߣ�
���磺��ͼ![]() ,AD��
,AD��![]() �ֳ�
�ֳ�![]() ��
��![]() ,��
,��![]() �ǵ���������,��
�ǵ���������,��![]() ��
��![]() ,��ôAD����
,��ôAD����![]() �������ָ��ߣ�
�������ָ��ߣ�
����������⣺
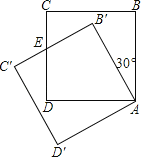
![]() ��ͼ
��ͼ![]() ,��
,��![]() ��,����B=40��,AD��
��,����B=40��,AD��![]() �������ָ���,��
�������ָ���,��![]() ����ADΪ�ױߵĵ���������,��
����ADΪ�ױߵĵ���������,��![]() ____�ȣ�
____�ȣ�
![]() ��
��![]() ��,��
��,��![]() ,
,![]() ,AD��
,AD��![]() �������ָ���,
�������ָ���,![]() �ǵ���������,��
�ǵ���������,��![]() ____��
____��
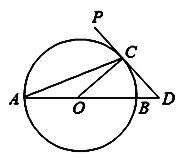
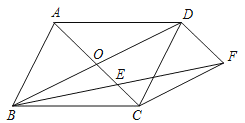
![]() ��ͼ
��ͼ![]() ,��
,��![]() ��,ADƽ��
��,ADƽ��![]() ,
,![]() ��֤AD��
��֤AD��![]() �������ָ��ߣ�
�������ָ��ߣ�
���𰸡���1��40����2��AB�ij�ֻ����3����3��������.
��������
��1�����������ָ������������ε����ʼ�����⣻
��2������![]() ��
��![]() ,�õ�
,�õ�![]() ���
���![]() ,�����BD���ٷ�����������ۼ�����⣻
,�����BD���ٷ�����������ۼ�����⣻
��3���������������ε��ж����������������ε����ʼ������.
![]() ��
��![]() �������ָ���,��
�������ָ���,��![]() ����ADΪ�ױߵĵ���������,
����ADΪ�ױߵĵ���������,
![]() ��
��![]() ,
,
![]() =40����
=40����
�ʴ�Ϊ40��
![]() ��
��![]() �������ָ���,
�������ָ���,![]() �ǵ���������,
�ǵ���������,
![]() ��
��![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
�ڵ���![]() ��,
��,
![]() ��
��![]() ʱ,
ʱ,![]() ��
��
![]() ��
��![]() ʱ,
ʱ,![]() ������,���������������
������,���������������
![]() ��
��![]() ʱ,
ʱ,![]() ��
��![]() ,���������������
,���������������
���AB�ij�ֻ����3��
�ʴ�Ϊ3��
![]() ֤����
֤����![]() ,
,
![]() ,
,
![]() ,
,
![]() ��
��![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() �ǵ���������,
�ǵ���������,
![]() ����
����![]() �������ָ��ߣ�
�������ָ��ߣ�