题目内容
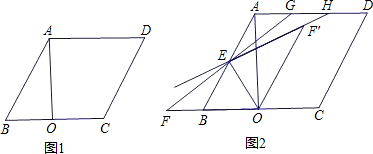
 如图,已知直线AB经过点C(1,2),与x轴、y轴分别交于A点、B点,CD⊥x轴于D,CE⊥y轴于E,CF与x轴交于F.
如图,已知直线AB经过点C(1,2),与x轴、y轴分别交于A点、B点,CD⊥x轴于D,CE⊥y轴于E,CF与x轴交于F.(1)当直线AB绕点C旋转到使△ACD≌△CBE时,求直线A8的解析式;
(2)若S四边形ODCE=S△CFD,当直线AB绕点C旋转到使FC⊥AB时,求BC的长;
(3)在(2)成立的情况下,将△FOG沿y轴对折得到△F′O′G′(F、0、G的对应点分别为F′、O′、G′),把△F′O′G′沿x轴正方向平移到使得点F′与点A重合,设在平移过程中△F′O′G′与四边形CDOE重叠的面积为y,OO′的长为x,求y与x的函数关系式及自变量x的取值范围.
分析:(1)已知C点的坐标,则已知CE,CD的长度,然后依据△ACD≌△CBE,即可求得OA,OB的长度,从而求得A,B的坐标,然后利用待定系数法即可求得AB的解析式;
(2)根据S四边形ODCE=S△CFD,可以得到△OGF≌△EGC,则EC=OF,而EC=OD,可以证得∠GFO=45°,在直角△OGF中,利用勾股定理即可求得GF的长,并且易证△BEC是等腰直角三角形,△BCG是等腰直角三角形,则BC=CG=GF,从而求解;
(3)O′的位置分两种情况:当△O′G′F′沿x轴正方向移动到使得点O′与点D重合时;当△O′G′F′从点O′与点D重合的位置继续沿x轴正方向移动到使得点F′与点A重合时,分别利用三角形的面积公式和梯形的面积公式即可求得函数解析式.
(2)根据S四边形ODCE=S△CFD,可以得到△OGF≌△EGC,则EC=OF,而EC=OD,可以证得∠GFO=45°,在直角△OGF中,利用勾股定理即可求得GF的长,并且易证△BEC是等腰直角三角形,△BCG是等腰直角三角形,则BC=CG=GF,从而求解;
(3)O′的位置分两种情况:当△O′G′F′沿x轴正方向移动到使得点O′与点D重合时;当△O′G′F′从点O′与点D重合的位置继续沿x轴正方向移动到使得点F′与点A重合时,分别利用三角形的面积公式和梯形的面积公式即可求得函数解析式.
解答:解:(1)∵CD⊥x轴,CE⊥y轴.x轴⊥y轴,
∴∠CDO=90°,∠CE0=900,∠EOD=90°.
∴四边形CDOE是矩形.
∴OD=EC,OE=DC.
∵C(1,2),
∴D(1,0),
E(O,2).
∴OD=1,OE=2.
∵△ACD≌△CBE.
∴EB=DC=0E=2.
∴OB=0E+EB=4.
∴B(O,4).
设直线AB的解析式为y=-2x+4.
因为直线AB经过点C(1,2),
所以2=k+4.k=-2
则直线AB的解析式为y=-2x+4;
(2)∵S△CFD=
FD•CD,S四边形ODCE=CD•CE,且S四边形ODCE=S△CFD,
∴
×2×FD=2×1,FD=2.
∴FO=FD-OD=1.
∵∠FGO=∠CGE,∠FOG=∠CEG=90°,FO=CE.
∴△OGF≌△EGC.
∴FG=CG,OG=EG=1.
在△FOG中,∠FOG=90°,FO=OG=1.
∴tan∠GFO=
=1.所以∠GFO=45°.
∴FG=
=
,
∵FC⊥AB,
∴∠BCF=90°,从而∠CBG=45°.
∴BC=GC.
∴BC=FG=
;
(3)因为∠CFA=45°,∠ACF=90°,所以∠CAF=45°,所以CD⊥AD,所以AD=FD=2
∵△F′O′G′与△FOG关于y轴对称,
∴F′O′=FO=I,
∴O′G′=OG=1.∠G′F′O′=∠CFD=45°
(I)当△G′O′F′沿x轴正方向移动到使得点O′与点D重合时.
0<x≤l,O′D=0D-0O′=1-x,DF′=O′F′-O′D=1-(1-x)=x
∵∠HDF′=900,∠HDF′=∠G′F′O′=450.
∴∠DHF′=450.
∴HD=DF′.
则y=
=
=-
x2+
(0<x≤1),
(II)当△O′G′F′从点O′与点D重合的位置继续沿x轴正方向移动到使得点F′与点A重合时,
l<x≤2,y=0
因此y与x之间的函数关系式为:y=
.
∴∠CDO=90°,∠CE0=900,∠EOD=90°.
∴四边形CDOE是矩形.
∴OD=EC,OE=DC.
∵C(1,2),
∴D(1,0),
E(O,2).
∴OD=1,OE=2.
∵△ACD≌△CBE.
∴EB=DC=0E=2.
∴OB=0E+EB=4.
∴B(O,4).
设直线AB的解析式为y=-2x+4.
因为直线AB经过点C(1,2),
所以2=k+4.k=-2
则直线AB的解析式为y=-2x+4;
(2)∵S△CFD=
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴FO=FD-OD=1.
∵∠FGO=∠CGE,∠FOG=∠CEG=90°,FO=CE.
∴△OGF≌△EGC.
∴FG=CG,OG=EG=1.
在△FOG中,∠FOG=90°,FO=OG=1.
∴tan∠GFO=
| GO |
| FO |
∴FG=
| OG |
| sin45° |
| 2 |
∵FC⊥AB,
∴∠BCF=90°,从而∠CBG=45°.
∴BC=GC.
∴BC=FG=
| 2 |
(3)因为∠CFA=45°,∠ACF=90°,所以∠CAF=45°,所以CD⊥AD,所以AD=FD=2

∵△F′O′G′与△FOG关于y轴对称,
∴F′O′=FO=I,
∴O′G′=OG=1.∠G′F′O′=∠CFD=45°
(I)当△G′O′F′沿x轴正方向移动到使得点O′与点D重合时.
0<x≤l,O′D=0D-0O′=1-x,DF′=O′F′-O′D=1-(1-x)=x
∵∠HDF′=900,∠HDF′=∠G′F′O′=450.
∴∠DHF′=450.
∴HD=DF′.
则y=
| (HD+O′G′)O′D |
| 2 |
| (x+1)(1-x) |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(II)当△O′G′F′从点O′与点D重合的位置继续沿x轴正方向移动到使得点F′与点A重合时,
l<x≤2,y=0
因此y与x之间的函数关系式为:y=
|
点评:本题考查全等三角形的性质,解直角三角形,求函数的解析式的综合应用,注意到分情况讨论是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 小汽车的速度是大货车速度的2倍,两车在匀速行驶过程中的最近距离是多少?
小汽车的速度是大货车速度的2倍,两车在匀速行驶过程中的最近距离是多少? =1.732)
=1.732) 小汽车的速度是大货车速度的2倍,两车在匀速行驶过程中的最近距离是多少?
小汽车的速度是大货车速度的2倍,两车在匀速行驶过程中的最近距离是多少? =1.732)
=1.732)

