题目内容
【题目】如图，已知AB∥CD，F为CD上一点，∠EFD=60°，∠AEC=2∠CEF，若6°＜∠BAE＜15°，∠C的度数为整数，则∠C的度数为 ．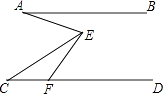 
【答案】36°或37°
【解析】解：如图，过E作EG∥AB，
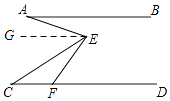
∵AB∥CD，
∴GE∥CD，
∴∠BAE=∠AEG，∠DFE=∠GEF，
∴∠AEF=∠BAE+∠DFE，
设∠CEF=x，则∠AEC=2x，
∴x+2x=∠BAE+60°，
∴∠BAE=3x﹣60°，
又∵6°＜∠BAE＜15°，
∴6°＜3x﹣60°＜15°，
解得22°＜x＜25°，
又∵∠DFE是△CEF的外角，∠C的度数为整数，
∴∠C=60°﹣23°=37°或∠C=60°﹣24°=36°，
所以答案是：36°或37°．
【考点精析】掌握平行线的性质是解答本题的根本，需要知道两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
