题目内容
(本题10分)小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: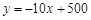 ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?
(成本=进价×销售量)
【答案】
(1)w 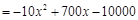 (20≤x≤32)
(20≤x≤32)
(2)当X=32时,W=2160
(3)3600
【解析】
试题分析:
解:
(1)由题意,得:w =
(x-20)·y=(x-20)·(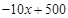 )
)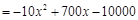 ,即w
,即w 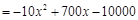 (20≤x≤32)
(20≤x≤32)
(2)对于函数w 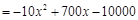 的图像的对称轴是直线
的图像的对称轴是直线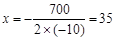 .
.
又∵a=-10<0,抛物线开口向下.∴当20≤x≤32时,W随着X的增大而增大,
∴当X=32时,W=2160
答:当销售单价定为32元时,每月可获得最大利润,最大利润是2160元.
(3)取W=2000得,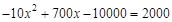
解这个方程得:x1 = 30,x2 = 40.
∵a=-10<0,抛物线开口向下.
∴当30≤x≤40时,w≥2000.
∵20≤x≤32
∴当30≤x≤32时,w≥2000.
设每月的成本为P(元),由题意,得:
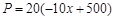
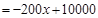
∵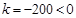 ,
,
∴P随x的增大而减小.
∴当x = 32时,P的值最小,P最小值=3600.
答:想要每月获得的利润不低于2000元,小明每月的成本最少为3600元.
考点:二次函数的应用
点评:二次函数的应用是中考的必考题型,考生在解此类问题时一定要注意分析求最大值和最小值所需要函数解决的问题。

练习册系列答案
相关题目
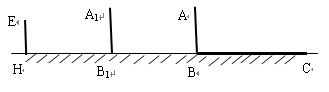
 点,并测得HB=6m.
点,并测得HB=6m.
 在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
在图中画出形成影子的光线,并确定路灯灯泡所在的位置G; 点,并测得HB=6m.
点,并测得HB=6m.
 在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
在图中画出形成影子的光线,并确定路灯灯泡所在的位置G; 点,并测得HB=6m.
点,并测得HB=6m.