题目内容
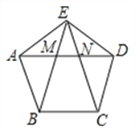
【题目】如图,正五边形的边长为2,连对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,则MN=__________;
【答案】3-![]()
【解析】根据正五边形的性质得到∠ABE=∠AEB=∠EAD=36°,根据三角形的内角和即可得到结论;由于∠AEN=108°﹣36°=72°,∠ANE=36°+36°=72°,得到∠AEN=∠ANE,根据等腰三角形的判定定理得到AE=AN,同理DE=DM,根据相似三角形的性质得到![]() ,等量代换得到AN2=AMAD;根据AE2=AMAD,列方程得到MN=3﹣
,等量代换得到AN2=AMAD;根据AE2=AMAD,列方程得到MN=3﹣![]() ;
;
解:∵∠BAE=∠AED=108°,
∵AB=AE=DE,
∴∠ABE=∠AEB=∠EAD=36°,
∴∠AME=180°﹣∠EAM﹣∠AEM=108°,
∵∠AEN=108°﹣36°=72°,∠ANE=36°+36°=72°,
∴∠AEN=∠ANE,
∴AE=AN,
同理DE=DM,
∴AE=DM,
∵∠EAD=∠AEM=∠ADE=36°,
∴△AEM∽△ADE,
∴![]() ,
,
∴AE2=AMAD;
∴AN2=AMAD;
∵AE2=AMAD,
∴22=(2﹣MN)(4﹣MN),
∴MN=3﹣![]() .
.
“点睛”此题主要考查了正多边形的性质和相似三角形的性质,根据三角形的内角和、相似三角形的性质即可得到结论.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目