Question

已知：在菱形ABCD中，AE⊥BC，垂足为点E，AB=13cm，对角线AC=10cm，那么AE=

120

13

cm．

Answer 1

分析：根据菱形的性质得出AO、AB的长，在RT△ABO中求出BO，进而得出BD，利用菱形面积等于对角线乘积的一半，也等于BC×AE，可得出AE的长度．

解答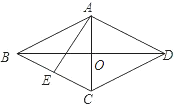：解：由题意得：AC=10cm，AB=13cm，
则AO=

1

2

AC=5cm，
在RT△ABO中，BO=

AB2-AO2

=12cm，
∴BD=24cm，
又∵S_ABCD=BC×AE=

1

2

AC×BD，
∴可求得AE=

120

13

cm．
故答案为：

120

13

．

点评：此题考查了菱形的性质，也涉及了勾股定理，要求我们掌握菱形的面积的两种表示方法，及菱形的对角线互相垂直且平分．