题目内容
已知:在菱形ABCD中,∠BAD=60°,把它放在直角坐标系中,使AD边在y轴上,点C的坐标为(2| 3 |
(1)画出符合题目条件的菱形与直角坐标系.
(2)写出A,B两点的坐标.
(3)设菱形ABCD的对角线的交点为P,问:在y轴上是否存在一点F,使得点P与点F关于菱形ABCD的某条边所在的直线对称,如果存在,写出点F的坐标;如果不存在,请说明理由.
分析:(1)本题可分两种情况,如图;
(2)过C作CF⊥y轴于F,∠CDF=60°,CF=2
,因此DF=2,CD=4.因此OA=OF-AF=8-(4+2)=2,因此A点坐标为(0,2).由于菱形的边长为4,因此将C点坐标向下平移4个单位就是B点的坐标(2
,4);
(3)在(2)中所作的F点其实就是P点关于CD的对称点,理由:根据菱形的性质可知:∠FAC=30°,因此在直角三角形FAC中,FC=
AC=PC,而∠DCF=∠DCP=30°,因此△CFE≌△CPE,因此CD垂直平分PF,即可得出P、F关于CD对称.
(2)过C作CF⊥y轴于F,∠CDF=60°,CF=2
| 3 |
| 3 |
(3)在(2)中所作的F点其实就是P点关于CD的对称点,理由:根据菱形的性质可知:∠FAC=30°,因此在直角三角形FAC中,FC=
| 1 |
| 2 |
解答:解:本题有两种情况:
第一种情况:(1)画图,如图所示.
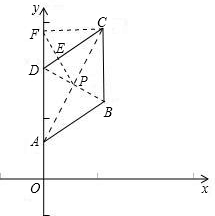
(2)过C作CF⊥y轴于F,∠CDF=60°,CF=2
,
∵tan60°=
=
,
=
,
∴DF=2,
CD=4.因此OA=OF-AF=8-(4+2)=2,因此A点坐标为(0,2).
由于菱形的边长为4,因此将C点坐标向下平移4个单位就是B点的坐标(2
,4);
则A(0,2),B(2
,4).
(3)F(0,8);
第二种情况:(1)画图,如图所示.
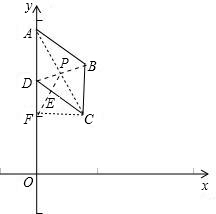
(2)A′(0,14),B′(2
,12)
(3)F′(0,8).
第一种情况:(1)画图,如图所示.

(2)过C作CF⊥y轴于F,∠CDF=60°,CF=2
| 3 |
∵tan60°=
| FC |
| DF |
| 3 |
2
| ||
| DF |
| 3 |
∴DF=2,
CD=4.因此OA=OF-AF=8-(4+2)=2,因此A点坐标为(0,2).
由于菱形的边长为4,因此将C点坐标向下平移4个单位就是B点的坐标(2
| 3 |
则A(0,2),B(2
| 3 |
(3)F(0,8);
第二种情况:(1)画图,如图所示.

(2)A′(0,14),B′(2
| 3 |
(3)F′(0,8).
点评:本题主要考查了菱形的性质、坐标与图形的性质、轴对称图形等知识点.

练习册系列答案
相关题目