��Ŀ����
��ͼ����C=90�㣬��A��B�ڡ�C�������ϣ�CA=30��CB=20������AB����P�ӵ�B��������ÿ��4����λ���ȵ��ٶ���BC�����˶�������Cֹͣ������P��B��C���㲻�غ�ʱ����PD�ABC��A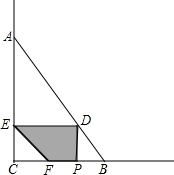 B��D����DE�AAC��E��FΪ����CB��һ�㣬�ҡ�CEF=��ABC�����P���˶�ʱ��Ϊx���룩��
B��D����DE�AAC��E��FΪ����CB��һ�㣬�ҡ�CEF=��ABC�����P���˶�ʱ��Ϊx���룩����1���ú���x�Ĵ���ʽ��ʾCE�ij���
��2�����F���B�غ�ʱx��ֵ��
��3������F���߶�CB��ʱ�����ı���DECP���ı���DEFB�ص�����ͼ�ε����Ϊy��ƽ����λ������y��x֮��ĺ�����ϵʽ��
��4����xΪij��ֵʱ����PD����D��E��F��BΪ������ı��μ������õ�����ͼ�Σ���������ͼ��ƴ�ɲ��ص�����϶��ͼ��ǡ���������Σ���ֱ��д�����з�������������xֵ��
��������1������֤����ABC�ס�DBP�ס�FEC�����ɵó�����ʽ�����ó���ʾCE�ij���
��2�����ݵ���F���B�غ�ʱ��FC=BC�����ɵó��𰸣�
��3������֤��Rt��DOE��Rt��CEF���ó�
=
�����ɵó�y��x֮��ĺ�����ϵʽ��
��4�����������α߳���ȵó��𰸣�
��2�����ݵ���F���B�غ�ʱ��FC=BC�����ɵó��𰸣�
��3������֤��Rt��DOE��Rt��CEF���ó�
| DO |
| DE |
| CE |
| CF |
��4�����������α߳���ȵó��𰸣�
��� �⣺��1����PD��BC��DE��AC���ҡ�C=90�㣬
�⣺��1����PD��BC��DE��AC���ҡ�C=90�㣬
���ı���DECPΪ���Σ�
��DE=PC��DP=EC��
�֡ߡ�CEF=��ABC��
���ABC�ס�DBP�ס�FEC��
��
=
=
��
��CA=30��CB=20��BP=4x��
��
=
=
��
��FC=9x��DP=EC=6x��
��2������F���B�غ�ʱ��FC=BC��
��FC=BC��
��9x=20��
��ã�x=
��
��3������F���P�غ�ʱ��4x+9x=20��
���x=
��
��FP=BC-FC-PB=20-9x-4x=20-13x��
��DE=PC=BC-PB=20-4x��
��y=��DE+FP��•DP•0.5=��20-4x+20-13x��•6x��0.5=3x��40-17x��=120x-51x2��
��
��x��
ʱ��
����DECP��DP��EC��
���DOE=��FEC��
��Rt��DOE��Rt��CEF��
��
=
��
��
=
��
��DO=
��20-4x����
��y=
DO•DE=
��
��20-4x����20-4x��=
��5-x��2��
��4������ͼ�ۣ���PD=PFʱ��6x=20-13x����ã�x=
����B��DEΪƴ�ɵ������Σ�
����ͼ�ܵ���F���P�غ�ʱ��4x+9x=20����ã�x=
����BDCΪƴ�ɵ������Σ�
����ͼ�ݣ���DE=PB��20-4x=4x����ã�x=
����DPFΪƴ�ɵ������Σ�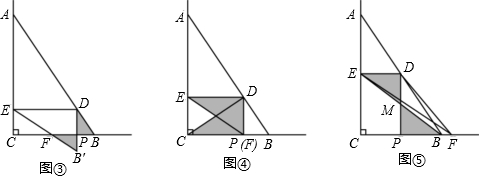
 �⣺��1����PD��BC��DE��AC���ҡ�C=90�㣬
�⣺��1����PD��BC��DE��AC���ҡ�C=90�㣬���ı���DECPΪ���Σ�
��DE=PC��DP=EC��
�֡ߡ�CEF=��ABC��
���ABC�ס�DBP�ס�FEC��
��
| FC |
| EC |
| DP |
| BP |
| AC |
| BC |
��CA=30��CB=20��BP=4x��
��
| FC |
| EC |
| DP |
| 4x |
| 30 |
| 20 |
��FC=9x��DP=EC=6x��
��2������F���B�غ�ʱ��FC=BC��
��FC=BC��
��9x=20��
��ã�x=
| 20 |
| 9 |
��3������F���P�غ�ʱ��4x+9x=20��
���x=
| 20 |
| 13 |
��FP=BC-FC-PB=20-9x-4x=20-13x��
��DE=PC=BC-PB=20-4x��
��y=��DE+FP��•DP•0.5=��20-4x+20-13x��•6x��0.5=3x��40-17x��=120x-51x2��
��
| 20 |
| 13 |
| 20 |
| 9 |
����DECP��DP��EC��
���DOE=��FEC��
��Rt��DOE��Rt��CEF��
��
| DO |
| DE |
| CE |
| CF |
��
| DO |
| 20-4x |
| 6x |
| 9x |
��DO=
| 2 |
| 3 |
��y=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 16 |
| 3 |
��4������ͼ�ۣ���PD=PFʱ��6x=20-13x����ã�x=
| 20 |
| 19 |
����ͼ�ܵ���F���P�غ�ʱ��4x+9x=20����ã�x=
| 20 |
| 13 |
����ͼ�ݣ���DE=PB��20-4x=4x����ã�x=
| 5 |
| 2 |

������������Ҫ���������������ε��ж��������Լ����ɶ����;��ε��������ж�����������ó���ABC�ס�DBP�ס�FEC�Լ�Rt��DOE��Rt��CEF�ǽ������Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����BAC=90�㣬AD��BC����ABE����ACF���ǵȱ������Σ���S��ABE��S��ACF���ڣ�������
��ͼ����BAC=90�㣬AD��BC����ABE����ACF���ǵȱ������Σ���S��ABE��S��ACF���ڣ�������| A��AB��AC | B��AD2��DC2 | C��BD2��DC2 | D��AC2��AB2 |
 14����ͼ����AOB=90�㣬��B=30�㣬��AOB����Կ������ɡ�AOB�Ƶ�O˳ʱ����ת���Ƕȵõ��ģ�����A����AB�ϣ�����ת�Ǧ��Ĵ�С������
14����ͼ����AOB=90�㣬��B=30�㣬��AOB����Կ������ɡ�AOB�Ƶ�O˳ʱ����ת���Ƕȵõ��ģ�����A����AB�ϣ�����ת�Ǧ��Ĵ�С������ 16����ͼ����C=90�㣬ADƽ�֡�CAB��DE��AB��E����DB=2DE=6cm����BC=
16����ͼ����C=90�㣬ADƽ�֡�CAB��DE��AB��E����DB=2DE=6cm����BC= ��֪����ͼ����C=90�㣬��C��AB�ཻ�ڵ�D��AC=5��CB=12����AD��
��֪����ͼ����C=90�㣬��C��AB�ཻ�ڵ�D��AC=5��CB=12����AD�� ��ͼ����AOB=90�㣬0C��OD���ҡ�BOC=
��ͼ����AOB=90�㣬0C��OD���ҡ�BOC=