题目内容
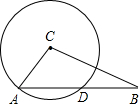已知：如图，∠C=90°，⊙C与AB相交于点D，AC=5，CB=12，求AD．
分析：过点C作CE⊥AB，垂足为E，由勾股定理，先求出AB的长，再由三角形的面积求出CE的长，再利用勾股定理得出AE，最后由垂径定理得出AD即可．
解答：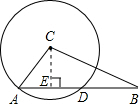
解：过点C作CE⊥AB，垂足为E，
∵∠C=90°，AC=5，CB=12，∴由勾股定理，得AB=13，
∵5×12=13•CE，∴CE=
，
∴由勾股定理，得AE=
，
∴由垂径定理得AD=
．
解：过点C作CE⊥AB，垂足为E，∵∠C=90°，AC=5，CB=12，∴由勾股定理，得AB=13，
∵5×12=13•CE，∴CE=
| 60 |
| 13 |
∴由勾股定理，得AE=
| 25 |
| 13 |
∴由垂径定理得AD=
| 50 |
| 13 |
点评：本题考查了垂径定理和勾股定理，解此类题目要注意将圆的问题转化成三角形的问题再进行计算．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
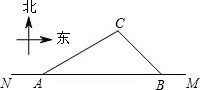，测得C在B的北偏西45°方向上．
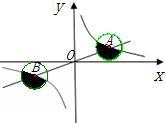11、已知，如图，正比例函数与反比例函数的图象相交于A、B两点，A点坐标为（2，1），分别以A、B为圆心的圆与x轴相切，则图中两个阴影部分面积的和为
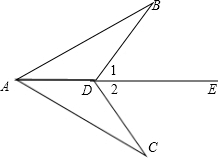已知，如图，∠1=∠2，
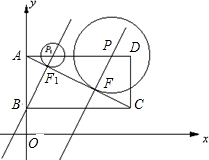已知，如图，直角坐标系内的矩形ABCD，顶点A的坐标为（0，3），BC=2AB，P为
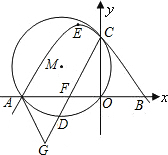于C点，⊙M经过原点O及点A、C，点D是劣弧