题目内容
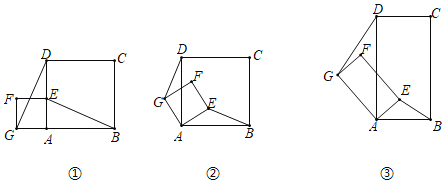
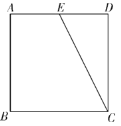
【题目】如图,在正方形ABCD中E为AD的中点,连接EC.
(1)作AEF∽DCE,点F在边AB上(要求:尺规作图,不写作法,保留作图痕迹):
(2)在(1)的条件下,连接CF,求证:AEF∽ECF.
【答案】(1)见解析;(2)见解析
【解析】
(1)作∠AEF=∠ECD,进而得出△AEF∽△DCE,即可得出答案;
(2)直接利用相似三角形的性质得出![]() ,再利用相似三角形的判定方法得出答案.
,再利用相似三角形的判定方法得出答案.
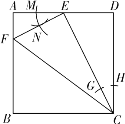
(1)如图,以C为圆心,以任意长为半径画弧,分别交CE、CD于G、H点;以E为圆心,以CG为半径画弧,交EA与M点;以M点为圆心,以GH为半径画弧,交前弧于N点;作射线EF交AB于F点,△AEF即为所求作的三角形;
(2)∵△AEF∽△DCE,
∴![]() ,
,
又∵E为AD的中点,
∴AE=ED,
∴![]()
∵∠DCE+∠DEC=90°,∠AEF=∠DCE,
∴∠AEF+∠DEC=90°,
∴∠FEC=90°,
∴∠A=∠FEC=90°,
∴△AEF∽△ECF

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
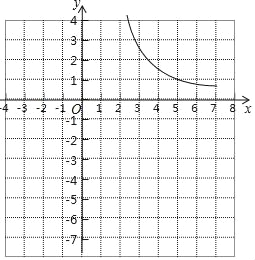
【题目】小邱同学根据学习函数的经验,研究函数y=![]() 的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
x | 1 |
|
|
| 3 | 4 | 5 | 6 | … |
y | ﹣1 | ﹣2 | ﹣3.4 | ﹣7.5 | 2.4 | 1.4 | 1 | 0.8 | … |
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)在图中补全当1≤x<2的函数图象;
(3)观察图象,写出该函数的一条性质: ;
(4)若关于x的方程![]() =x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .
=x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .